工程能力指数とは、ある工程が、設計仕様(規格)を満たす製品をどれだけ安定して生産できるかを示す指標です。
第24回~第30回のQC検定3級では以下のように出題されます。
| 試験(QC検定3級) | 第24回 | 第25回 | 第26回 | 第27回 | 第28回 | 第30回 |
| 工程能力指数 | 1問 | × | 1問 | × | × | 1問 |
管理図は第24回~第30回のQC検定3級では約50%の確率で出題されます。
出題頻度がそこまで高くないにも関わらず、勉強する範囲が少し広く、QC検定3級の中では問題のレベルが高いです。
だから、まずはポイントをしっかりと押さえ、勉強時間に余裕があれば全体を学ぶ事をおすすめします。
出題傾向とポイント
QC検定3級では以下の3点について問われる傾向があります。
- 工程能力指数についての理解と計算
- Cp、Cpkの評価
- ヒストグラムで工程能力指数を評価
工程能力指数(Cp、Cpk)について
冒頭で少し説明させて頂いた通り、工程能力指数とは、ある工程が、設計仕様(規格)を満たす製品をどれだけ安定して生産できるかを示す指標です。
工程能力指数では、工程が安定状態のときにどの程度のバラツキで品質を実現できるか確認する時に使用します。
指標は以下の2つがあります。
Cp
Cpは工程のバラツキが規格幅に対して、どの程度収まるかを評価します。
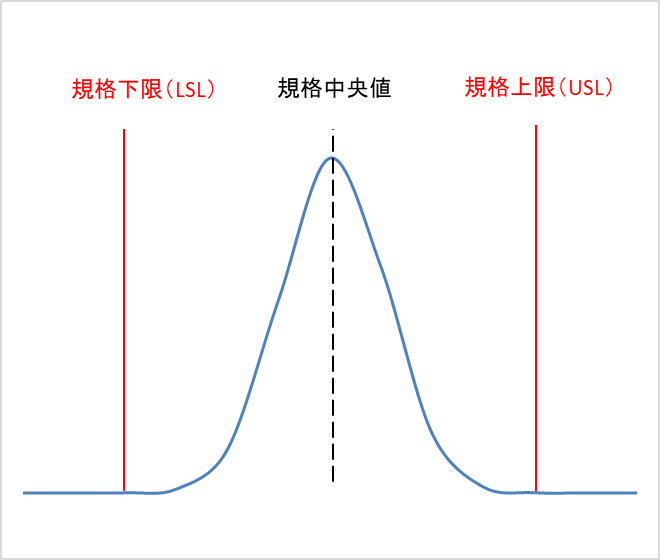
Cpのデータ分布の中心は、必ず規格中央値と同じになります。
仮に測定を行った母集団が規格から外れていたとしても、測定結果のバラツキが小さければCp値は高くなります。
【計算式】
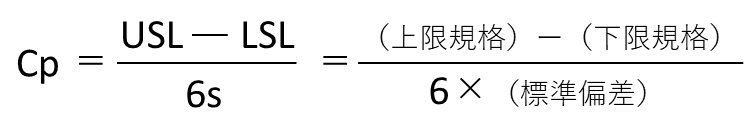
USL(SU): 上限規格
LSL(SL) : 下限規格
s(σ) : 標準偏差
Cpk
工程のバラツキに加え、データ分布の中心が規格中央値からどれだけズレがあるかも評価しています。
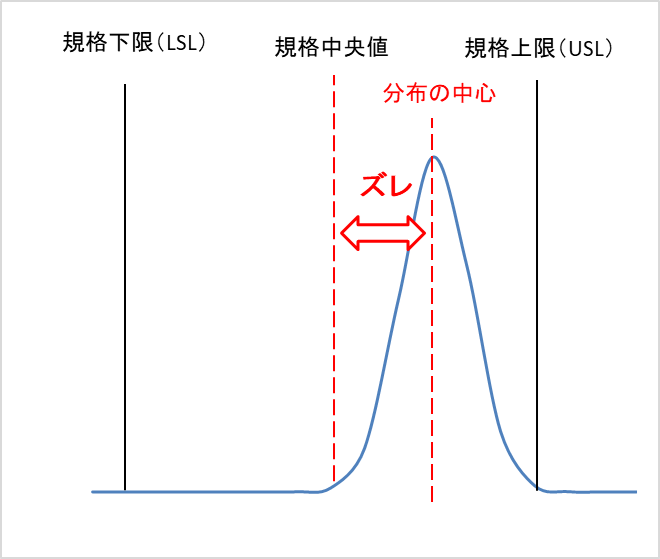
工程のバラツキが小さく、測定結果が全て規格内であっても、データ分布の中心と規格中央値のズレが大きければCpk値は低くなります。
【計算式】
Cpkはデータ分布の平均値と規格中央値のズレも評価する上で、平均値が規格中央値超えているか(平均値が規格上限側にズレているか)、または平均値が規格中央値を下回っているか(平均値が規格下限側にズレているか)で計算式が少し変わります。
・平均値が規格中央値より大きい場合
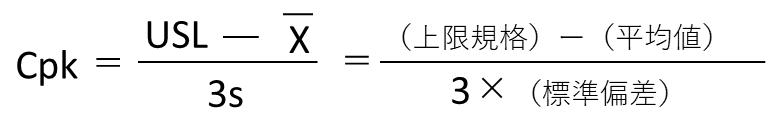
・平均値が規格中央値より小さい場合

USL(SU): 上限規格
LSL(SL) : 下限規格
s(σ) : 標準偏差
Cp、Cpkの評価
上記の計算式で求められたCpとCpkの値で、その工程の生産能力の指標になります。
Cp(Cpk)の値に対して、生産能力や必要な対応は以下の通りです。
| Cp(Cpk) | 工程能力 | 対応 |
| Cp≧1.67 | 工程能力は十分過ぎる | バラツキがもう少し大きくなっても心配ないので、管理の省略化やコスト低減方法を検討。 |
| 1.67>Cp≧1.33 | 工程能力は十分 | 理想的な状態なので維持する。 |
| 1.33>Cp≧1.00 | 工程能力は十分とは言えないが、まずますである | 工程管理をしっかりと行い管理状態に保つ。 Cpが1に近づくと不適合品発生の恐れがあるので、必要に応じて対応する。 |
| 1.00>Cp≧0.67 | 工程能力は不足している | 不適合品が発生している。 全数検査や工程管理の改善が必要。 |
| 0.67>Cp | 工程能力は非常に不足している | とても品質を満足する状態ではないので、原因を追及し品質改善を行い、緊急対策が必要。または規格を再検討する。 |
またCp(Cpk)においての不良発生確率は以下の通りです。
| Cp(Cpk) | S(σ) | 不良発生率 |
| Cp=0.67 | ± 2s | 約4.6% |
| Cp=1.00 | ± 3s | 約0.3% |
| Cp=1.33 | ± 4s | 約0.006% |
| Cp=1.67 | ± 5s | 約0.00006% |
データ分布(ヒストグラム)を視覚的に評価
上記2つの出題傾向とは逆説的に、データの分布やヒストグラムなどの図表からCpやCpkの値やどんな対応が必要か問われる事もあります。
【例題1】
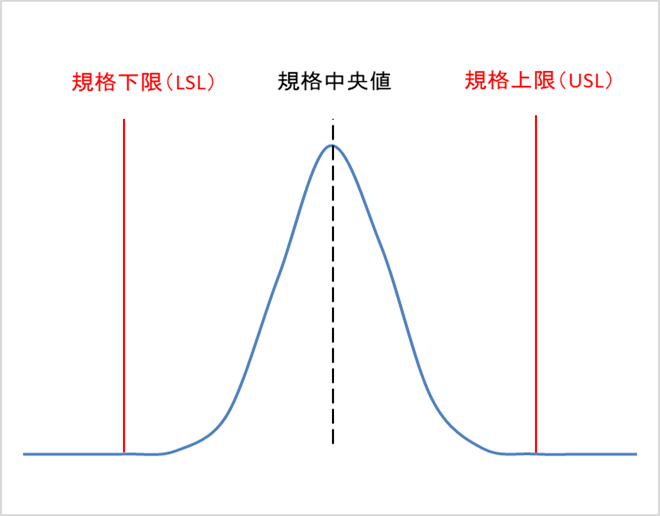
こちらのデータ分布では以下の2点に注目します。
・データ分布の中心(平均)が、規格中央値と近い
・データの分布の幅が、規格の幅に対して十分に狭く余裕がある
この場合、工程能力は十分または十分過ぎるになる可能性が高いです。
【参考の工程能力】
・Cp ≧ 1.33
・Cpk ≧ 1.33
【例題2】
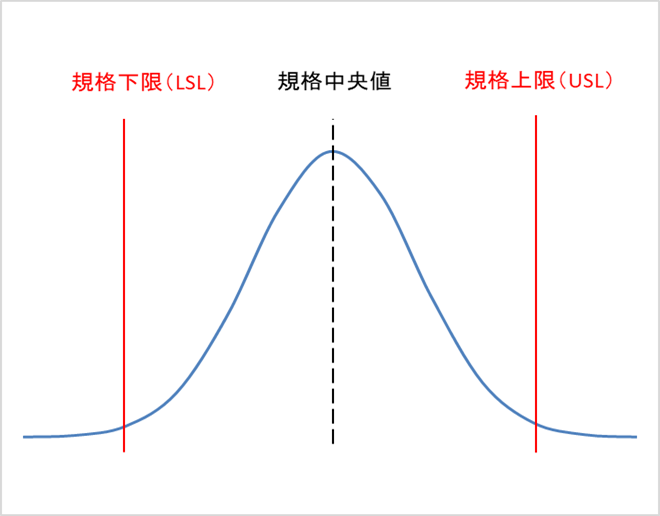
こちらのデータ分布でも以下の2点に注目します。
・データ分布の中心(平均)が、規格中央値と近い
・データの分布の幅が、規格の幅に対して広い
この場合、工程能力は不足している、または非常に不足しているになる可能性が高いです。
【参考の工程能力】
・Cp < 1.00
・Cpk < 1.00
【工程への対応】
Cp、Cpkが1.33以下なので、工程改善の検討が必要です。
データ分布の中心の位置は規格中央値と近いので、データの分布の幅が狭くなる処置が必要になります。
【例題3】
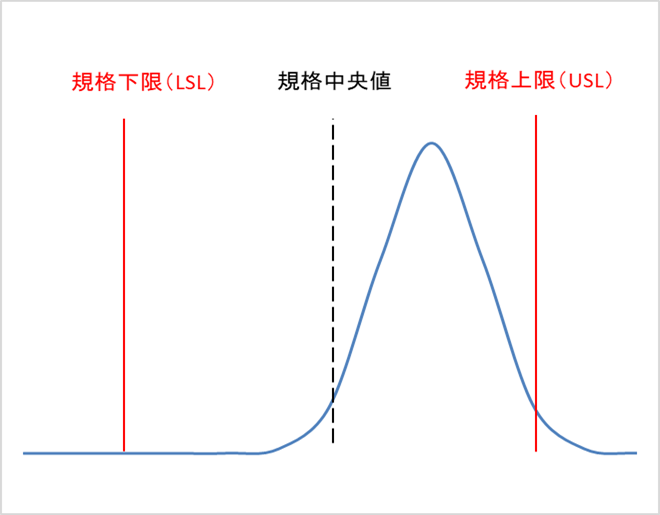
こちらのデータ分布でも以下の2点に注目します。
・データ分布の中心(平均)が、規格中央値とズレている
・データの分布の幅が、規格の幅に対して十分に狭い
この場合、工程能力は不足している、または非常に不足しているになる可能性が高いです。
【参考の工程能力】
・Cp ≧ 1.33
・Cpk < 1.00
【工程への対応】
Cpは問題ありませんがCpkが1.33以下なので、工程改善の検討が必要です。
データの分布の幅は十分に狭い(Cp≧1.33)ので、ここに対しての改善は必要ありません。
データ分布の中心(平均)の位置については、規格中央値からズレが見られるので、ここについて処置が必要になります。
その他
ここからはQC検定にはあまり出題されませんが、工程能力指数の理解に必要と思った内容、書かせて頂きます。
標準偏差とは
ウィキペディア(Wikipedia)では標準偏差について、以下の通りに説明しています。
標準偏差(ひょうじゅんへんさ、(英: standard deviation, SD)とは、データや確率変数の、平均値からの散らばり具合(ばらつき)を表す指標の一つである。
ウィキペディア(Wikipedia)
標準偏差 – Wikipedia
ここで大切なのが「平均値からの散らばり具合(ばらつき)を表す指標の一つ」の部分です。
前回のヒストグラム①では視覚でヒストグラムのバラツキを確認していましたが、標準偏差では数値でバラツキを確認する事ができます。
標準偏差の計算方法
標準偏差の計算方法を、前回のヒストグラム①の大根の長さを例にして説明します。
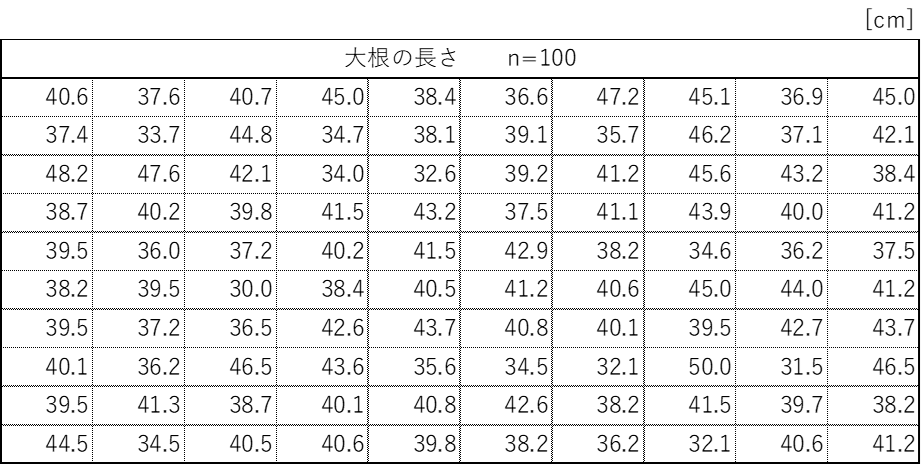
上表の平均値はXbar=40.0になります。
①偏差平方和の求め方
偏差平方和とは「データと平均値の差を2乗した値の合計の値」の事です。
n=100の場合だと以下の通りになります。
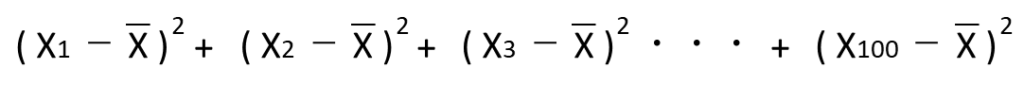
以下は公式と今回のデータの計算結果になります。
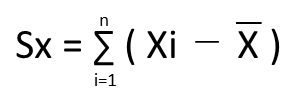
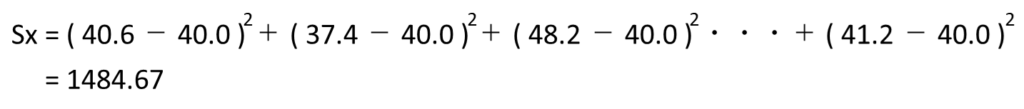
②不偏分散の求め方
不偏分散(Vx)とは、標本から母集団の分散を推定する時に用いられます。
※標本・・・サンプルデー(例:大根の長さ n=100)
母集団・・・調査対象全てを含む集団(例:全ての大根の長さ)
公式と今回のデータからの計算結果は以下の通りです。
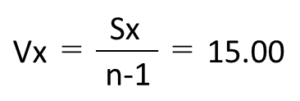
③標準偏差の求め方
標準偏差は以下の公式で求めます。
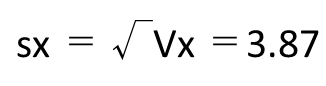
求めた標準偏差s(sx)から、バラツキを確認する事ができます。
まずヒストグラムにXbar(平均値)の線を引きます。
そして、Xbar ± s、Xbar ± 2s、Xbar ± 3sと線を引きます。
Xbar ± sの範囲で約68%
Xbar ± 2sの範囲で約95%
Xbar ± 3sの範囲で約99.7%
それぞれの確率でデータがその間に収まります。
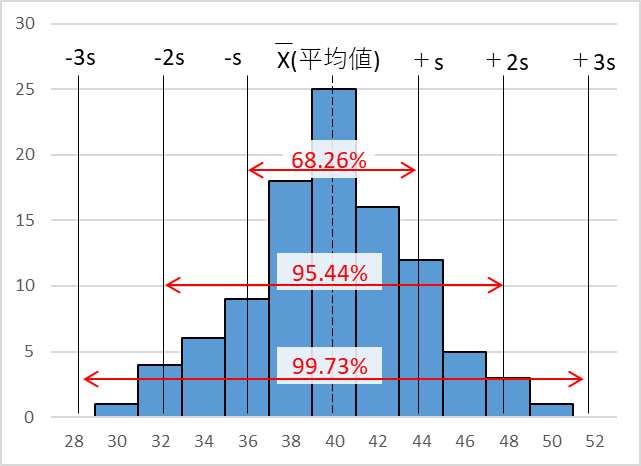
今回のデータはsx = 3.87なので、同じ条件で抜き取りで測定すると
Xbar ± s = 40.0 ± 3.87 の範囲で約68%
Xbar ± 2s = 40.0 ± 7.74 の範囲で約95%
Xbar ± 3s = 40.0 ± 11.61 の範囲で約99.7%
の確率で各範囲にデータが収まると考えられます。
工程能力指数(Cp)の片側(上限・下限)規格の計算方法
工程能力指数(Cp)は、両側規格と片側(上限・下限)規格で公式が違います。
[規格の例] 両側規格: ± 1.0 上限規格:0 / -1.0 下限規格:-1.0 / 0
公式は以下の通りです。
[両側規格の場合]
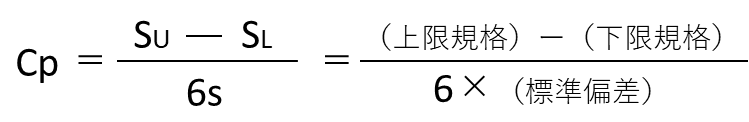
[上限規格の場合]
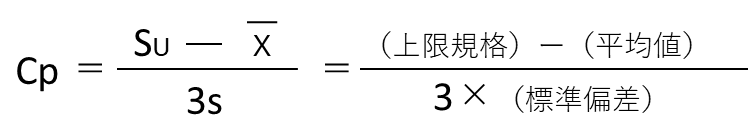
[下限規格の場合]
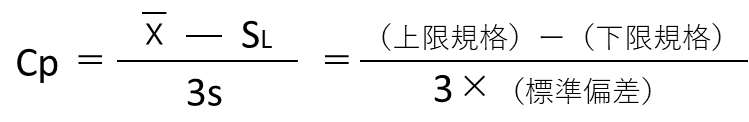
片側(上限・下限)規格の計算式はCpkと同じになります。



コメント