この記事では、QC検定3級のテスト対策として散布図の練習問題を作成しました。
良ければ、練習として解いてみて下さい。
QC検定3級向けの散布図の解説は以下の記事で投稿しておりますので、よければご覧ください。
問題
問1 ○✕問題
次の文章で正しければ〇、間違えなら✖と回答せよ。
(a)
散布図の分布が太く楕円に近いていくと2つの変数は強い相関と言い、散布図の分布が長細く直線に近ければ弱い相関と言う。
(b)
散布図が右肩上がりの分布は正の相関と言い、右肩下がりの分布は負の相関と言う。
(c)
相関係数rは必ず0≦1の範囲になる。
(d)
相関係数rが0に近づく程、散布図は負の相関が強くなり、1に近づくほど正の相関が強くなる。
問2 散布図の比較
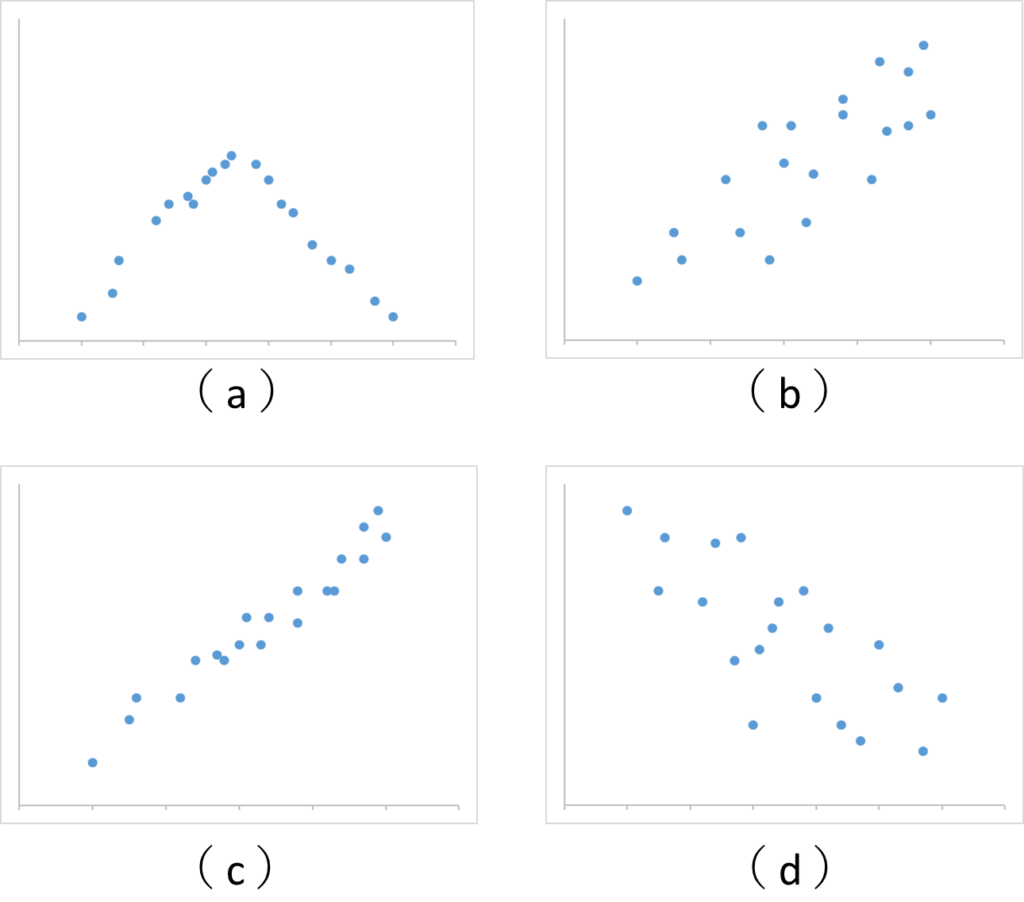
次の散布図(a)~(d)を相関係数rが大きい順に並べよ。
問3 相関係数rの計算
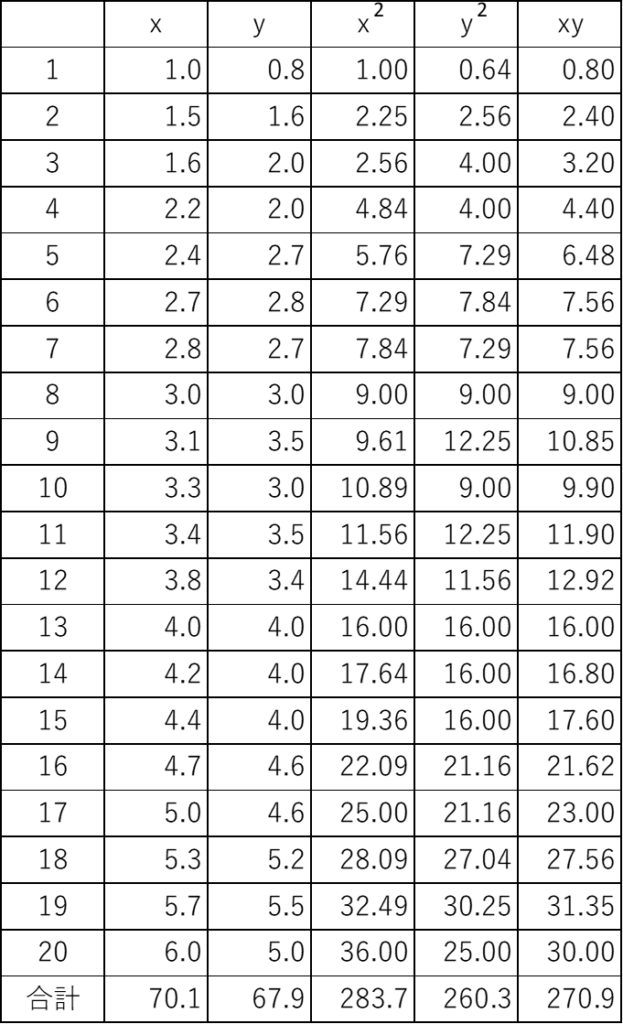
以下の「xとyのデータとその補助表」から相関係数rを求めよ
※答えは小数第二まで求める事。
解答
問1 解答
QC検定3級では問題に散布図が無く、問1のように文章で問われる事もありますので、相関の範囲を理解し、また文章からどんな散布図かイメージできるようにしておきましょう。
(a):✖
散布図の分布が太く楕円に近いと言うことは点(プロット)は散らばっているので弱い相関、細長い直線なら点は集中しているので強い相関になります。
(b):〇
問題の通り、右肩上がりなら正の相関、右肩下がりなら負の相関になります。
(c):✖
相関係数rは-1 ≦ r ≦ 1の範囲になります。
補足ですが相関係数rは-1に近づくほど負の相関が強くなり、1に近づくほど正の相関が強くなります。
ただし相関係数rは散布図の傾きでは無いので注意しましょう。
例えば、左の散布図の方が傾きが小さいですが、正の相関は左の散布図の方が強いです。
(d): ✖
(c)の解答の通り、-1に近づくほど負の相関が強くなります。
問2 解答
答え(相関係数が大きい順):(c)⇒(b)⇒(a)⇒(d)
下記の散布図の解説の例題と、解き方は同じになります。
QC検定3級 QC七つ道具 散布図 | アンキロぱぱのQC検定3級合格のためのブログ (ankiropapa.com)
ポイントは2つあります。
[ポイント]
・散布図が正の相関、負の相関、相関なしか考える。
・他の散布図と比較し、相関の強さを考える。
まずはそれぞれが何の相関になるもしくは近いか考えます。
(a)は相関なしに近く、(b)と(c)が正の相関、(d)が負の相関になります。
相関係数は相関なしに近いと0に近く、負の相関は符号がーになり、正の相関は符号が+になるので、(b)(c)が1番目か2番目のどちらかになり、(a)が3番目、(d)が4番目が確定します。
次に(b)と(c)の相関の強さを比較すると、(c)の方が細い直線で点が集中しているのでこちらの方が相関が強くなります。
正の相関が強いと相関係数は1に近くなるので、
(c)⇒(b)⇒(a)⇒(d)の順番になります。
今回の問題では(a)をr=0に近いと判断することがポイントだと思います。
プロットが散らばっている散布図や、左右対称のU字・V字(逆向きも含みます)の散布図をr≒0(相関なし)と判断できるようにしておきましょう。

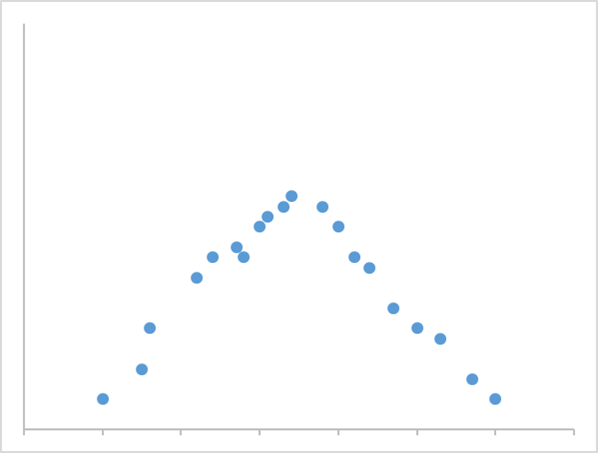
問3 解答
まず、相関係数rは以下の公式で求めます。
また上記の平方和Sxy、Sxx、Syyの公式は以下の通りになります。
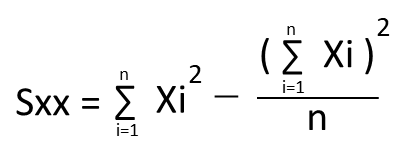
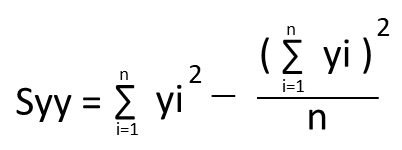
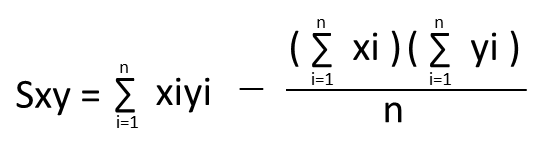
表にはxやyなどの合計も載っているので、上記の平方和の公式に各数値を代入します。
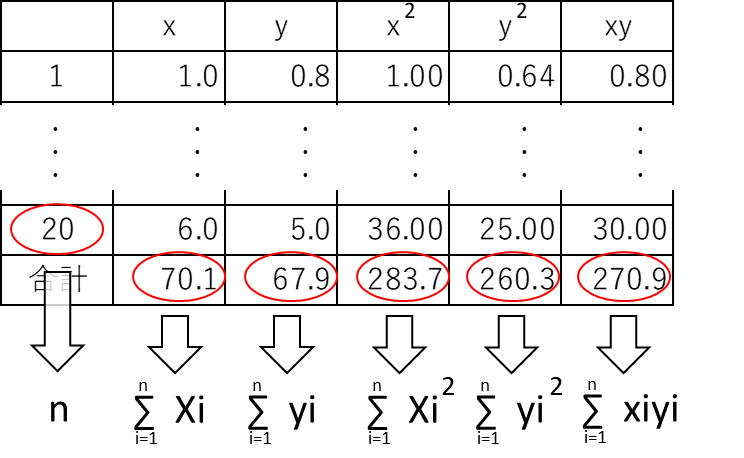
それぞれを平方和の公式に代入すると以下の通りになります。
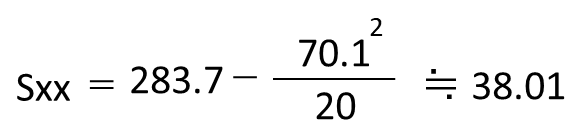
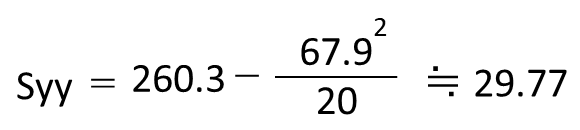
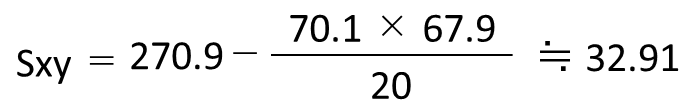
最後に相関係数rの公式にSxx、Syy、Sxyの値を代入します。
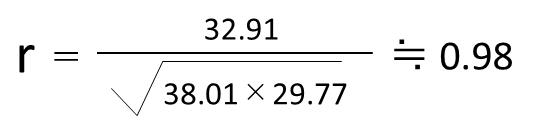
よって答えは上記のr=0.98になります。
今回の問題のように、Sxx、Syy、Sxyを問われる事は、QC検定3級ではほとんどありません。
※第24回~30回て1度、Sxyが出題されただけです。
ただし相関係数rは第24回~30回で3度出題されてあるので、この公式は覚えておくことをお勧めします。

最後に
問1、問2はQC検定3級の散布図で基本的な内容になるので、しっかりと理解しましょう。
問3はそこまで出題される確率は高くないので、余裕があれば解けるようにしておきましょう。
ただし相関係数rの公式は2回に1回の頻度で出題されるので、覚えておくことをお勧めします。
また散布図では√の計算があるので、電卓は必ず√計算ができる物を用意しておきましょう。





コメント