こちらの記事では、QC検定3級「手法編」の計算式以外の要点になるワードをまとめております。
これから手法編を勉強するのに全体的な内容を把握したい方や、試験直前に最後の見直しをしたい方は是非ご活用下さい。
この記事は、QC検定3級を受ける上で最低限必要と思ったワードをピックアップています。
また、計算式については別の記事にまとめています。良ければこちらもご覧下さい。
もう少し詳しく学習・見直しされたい方は、そのテーマの解説や練習問題の記事も張っておりますので、良ければそちらもご覧下さい。
データの取り方・まとめ方
QC検定3級での出題傾向は、基本統計量の計算方法をメインに、時々、データの種類やサンプリングについて出題されます。
データの種類
データは以下の4種類です。それぞれ区別できるようにしておきましょう。

サンプリング
サンプリングからデータを収集(測定)する事で、母集団の傾向を推測する事ができます。
ただし、データには必ずバラツキがあります。バラツキの種類と関係は以下の通りです。
データのバラツキ = サンプリング誤差のバラツキ + 測定誤差のバラツキ
基本統計量
こちらは計算がメインで出題されます。計算方法については冒頭の公式をまとめた記事や以下のデータの取り方・まとめ方の記事をご覧下さい。
計算式以外ではメディアン(Me)の出題頻度が高いです。
データの中央値がメディアンになりますが、データ数が奇数の時と偶数の時で求め方が変わるので注意しましょう。
奇数・・・中央値
偶数・・・真ん中2個の平均値
具体的な解き方や練習問題のありますので、こちらも是非ご覧下さい。
QC七つ道具
QC七つ道具はグラフ、特性要因図、散布図、チェックシート、パレート図、管理図、ヒストグラムの事で、手法分野では50%~80%、全体で考えても25%~44%に当たり、QC検定3級の目玉になります。
合格するには、QC七つ道具を理解する事は必須なのでしっかりと覚えましょう。
※管理図はQC七つ道具ですが、QC検定3級では独立した項目になっています。
層別
層別とはデータを、作業者、日付、設備、生産時の温度、生産条件などの項目に分けて比べる事で違いを見つける事ができる手法で、他のQC七つ道具の前準備として活用されます。
層別は、結果の違いから見る方法と、原因の違いから見る方法があります。
【結果(特性)の層別】
結果(特性)を層別する事で、原因(要因)の違いを見る事ができます。
【原因(要因)の層別】
原因(要因)する事で、結果(特性)の違いを見る事ができます。
具体的な解き方や練習問題のありますので、こちらも是非ご覧下さい。
グラフ
グラフとはデータを分かり易く表した図形の事です。
QC検定3級では棒グラフ、折れ線グラフ、円グラフ、帯グラフ、レーダーチャートの5種類が出題されます。
| No | グラフ名 | 使用目的 |
|---|---|---|
| 1 | 棒グラフ | 項目ごとの数値の大小を比較する |
| 2 | 折れ線グラフ | 確認したい特性を時間変化で傾向をつかむ |
| 3 | 円グラフ | 全体に対して、各項目の構成比率を確認する |
| 4 | 帯グラフ | 複数系列の項目で構成比率を比較する |
| 5 | レーダーチャート | 複数の項目に対して、項目間のバランスや達成の程度をつかむ |
具体的な図解や練習問題のありますので、こちらも是非ご覧下さい。
特性要因図
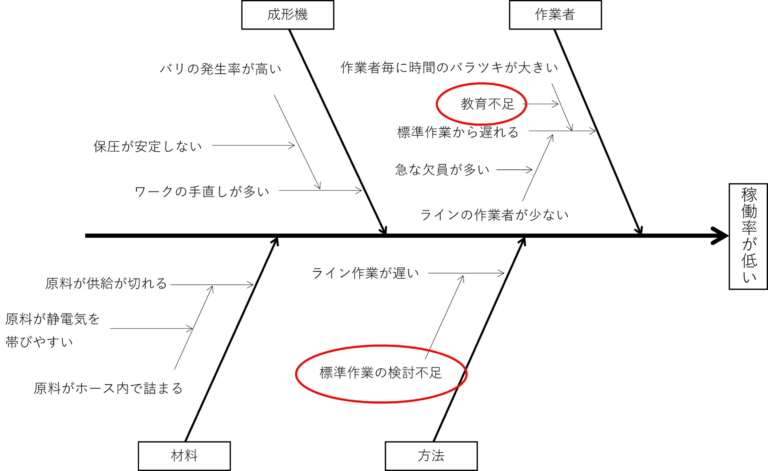
特性要因図とは、特性(結果)と、特性に対して影響を与えていると要因(原因)との関係を、言語データとして図で整理したもので、図の形から魚の骨とも言われます。
特性とは、生産や作業など生まれた結果の事で、特性要因図の背骨に当たります。
要因とは、特性に対して影響を与えている原因の事で、特性要因図では大骨、中骨、小骨、に当たります。
また、要因には人(Man)、機械(Machine)、材料(Material)、方法(Method)の4Mを当てはめるのが一般的です。
具体的な解き方や練習問題のありますので、こちらも是非ご覧下さい。
散布図(相関分析)
散布図とは、2つの変数の相関関係を視覚化する事を目的とした手法です。
QC検定3級では「散布図から相関係数の大きさを推測する事」や「表から相関の強さや向きを計算する事(相関分析)」などが出題されます。
この記事では計算がメインの相関分析は省略しておりますので、そちらについては冒頭の公式をまとめた記事や以下の散布図と相関分析の記事をご覧下さい。
相関の強さ
散布図の分布形状が、細長く集中し1本の線に近づけば強い相関で、逆に太く楕円のように散らばると弱い相関となります。
弱い相関より分布が散らばり、相関が見られない事を相関なしと言います。
相関の向き
散布図が右肩上がりの分布は正の相関、逆に右肩下がりの分布は負の相関といいます。
相関の数値化
相関の強さや向きは数値で表す事ができます。これを相関係数[r]と言います。
相関係数[r]は -1 ≦ 0 ≦ 1 の範囲となります。
1に近ければ正の相関は強く、-1に近ければ負の相関が強くなります。また0の場合は相関なしとなります。
具体的な解説や練習問題はこちらにありますので、是非ご覧下さい。
チェックシート
チェックシートとは、調査や点検の項目をあらかじめ決めておき、不具合調査や作業時などにチェックするためのシートです。
チェックシートには、調査用が4つと点検用が1つの計5種類があります。
| 種類 | 用途 |
|---|---|
| 不適合項目調査用チェックシート | あらかじめ予想できる不適合(不具合)を項目にし、発生件数を調査 |
| 不適合要因調査用チェックシート | 不適合の発生要因を層別し調査 |
| 欠点位置調査用チェックシート | 製品図に直接、欠点(不具合)をプロットし、欠点の発生を調査 |
| 度数分布調査用チェックシート | 数値化できる特性をあらかじめ区分し、ばらつきを調査 |
| 点検用チェックシート | 設備や製品などに正常か、または安全かを確認 |
チェックシートの詳細な説明や練習問題はこちらにありますので、是非ご覧下さい。
パレート図
パレート図とは、全体の中で何の原因や事象が大きな影響を占めているかを明確にする為の手法です。
大きく影響がある事象を取り上げる事で、効率的に改善する事ができます。
この考え方を重点指向と言います。
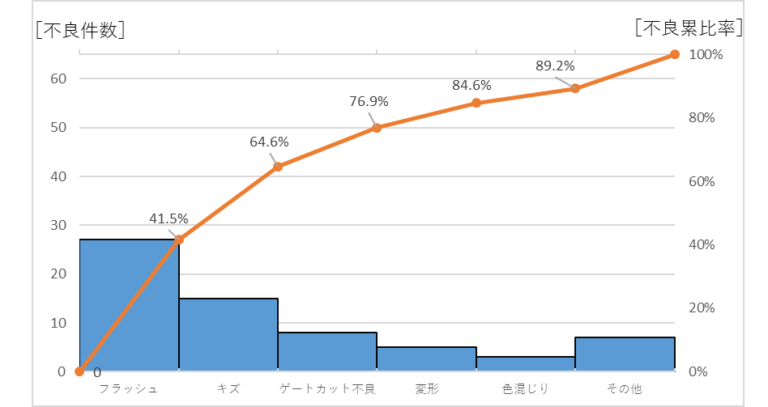
パレート図の形
パレート図は不具合項目や作業項目などを層別したものを横軸にし、不良数、作業時間、金額(不良の損金失額)などを縦軸にします。
横軸は大きい順に並べ、棒グラフで表示します。次に横軸の項目を累積和でプロットして折れ線グラフで表示します。
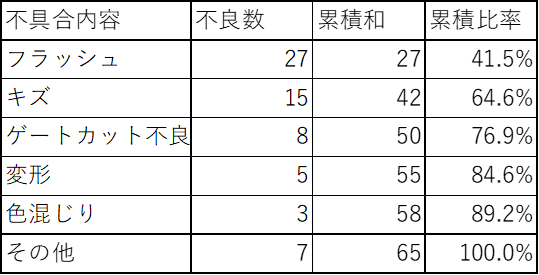
データ表(補助表)
パレート図を作成する前にデータ表(補助表)を作成します。
データ表の度数が大きい順になるように並べます。
度数の隣の項目は度数の累積和、その隣に累積比率を追加します。
パレート図の具体的な解説や練習問題のありますので、こちらも是非ご覧下さい。
ヒストグラム
ヒストグラムとは、品質特性値のバラツキをデータの分布で表し、規格値との関係や不適合発生状況などを視覚的に認識するための手法です。
分布の形
ヒストグラムの分布の形にはそれぞれ特徴があります。
| 一般型 | 歯抜け型 | 絶壁型 |
|---|---|---|
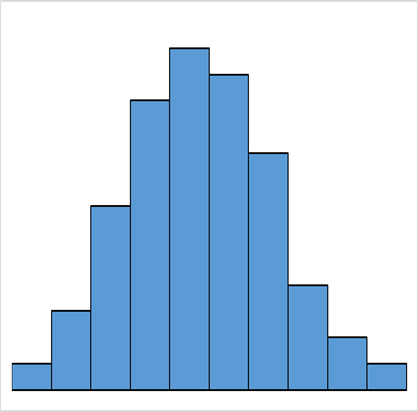 | 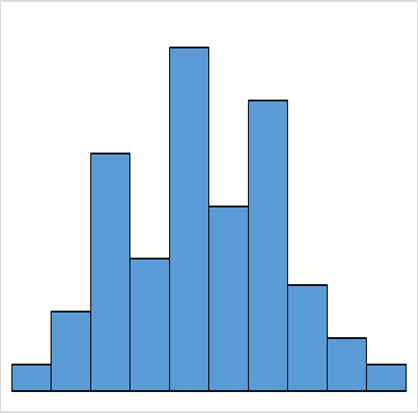 | 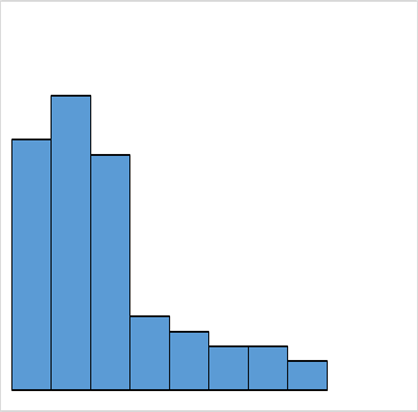 |
| 工程が安定 | 測定者の測定方法や読み方にクセがある | 規格外を選別で取り除いり、測定のごまかしや測定ミス |
| 高原型 | ふた山型 | 離れ小島型 |
|---|---|---|
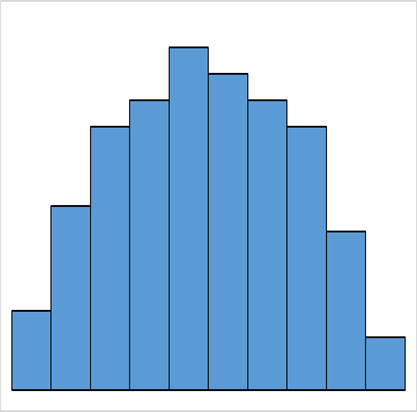 | 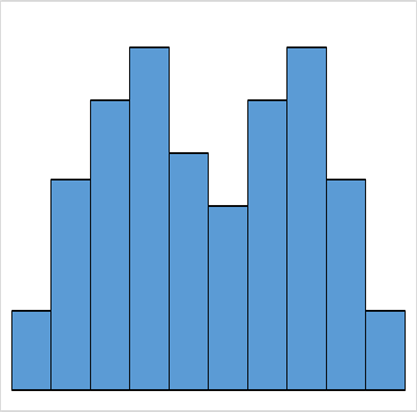 | 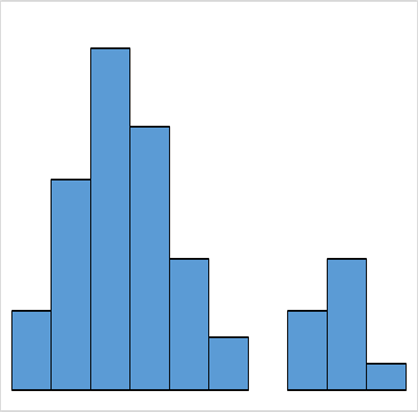 |
| 平均値が異なる複数の分布が混ざっている | 平均値が異なる2つの分布が混ざっている | 異なった分布のデータが少量混ざっている |
バラツキ方
ヒストグラムには理想的なバラツキ方と理想的でないバラツキ方があります。
以下のバラツキ方は理想的でないバラツキ方です。
| バラツキ方 | 分布の特徴 | 処置 |
|---|---|---|
| 片側に寄っている | バラツキの幅は理想に近いが、上下限どちらかに寄っている | 分布の平均値を中心に近づくように工程を調整する |
| 規格上下限に余裕がない | 理想な分布に対してバラツキの幅が広く、規格内だが上下限近くまで分布が広がっている | バラツキの幅が広くなる原因を調査し対策する |
| 規格上下限に余裕があり過ぎる | 理想な分布に対してバラツキの幅が狭く、分布と規格上下限までの隙間が大きい | 規格上下限の幅を狭くする。 または、工程の一部を省力化するなど、コストダウンを図る。 |
パレート図の詳細な解説や練習問題はこちらにありますので、是非ご覧下さい。
新QC七つ道具
QC七つ道具と同様に、新の問題点を明確にするために品質管理でよく用いられるのが新QC七つ道具です。
新QC七つ道具を用いることで、言語データについて解析や情報の見える化を行うことができる手法です。
それぞれの名前と図が一致するように覚えておきましょう。
| 名前 | 図 |
|---|---|
| 親和図法 | 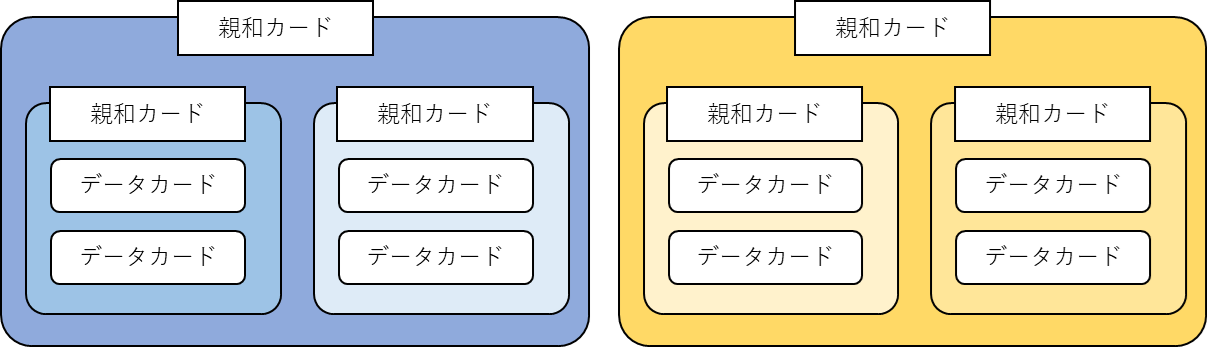 |
| 系統図 | 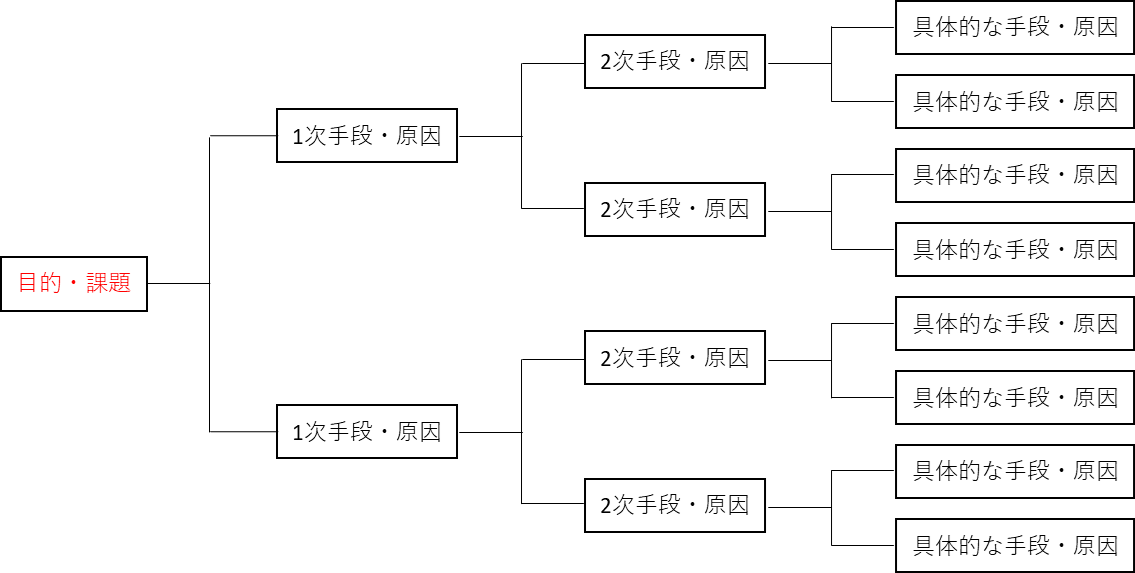 |
| 連関図法 | 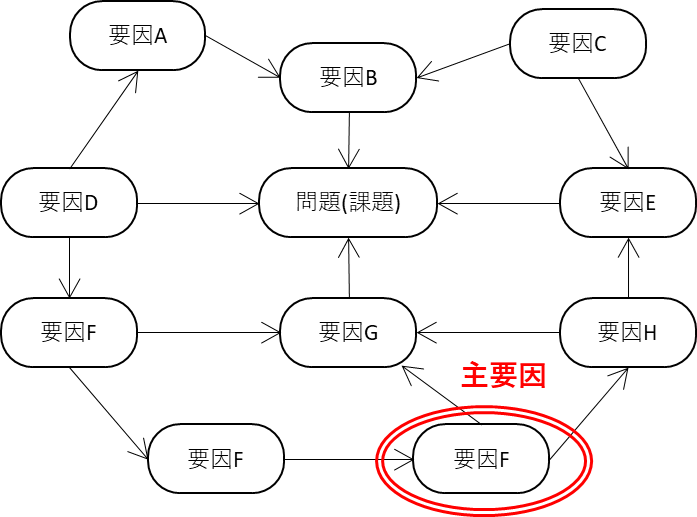 |
| アローダイヤグラム法 | 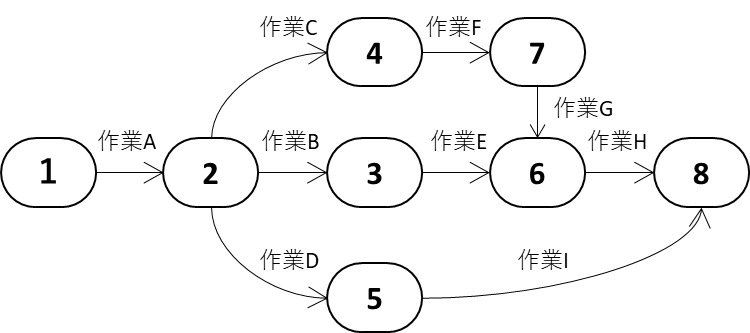 |
| PDPC法 | 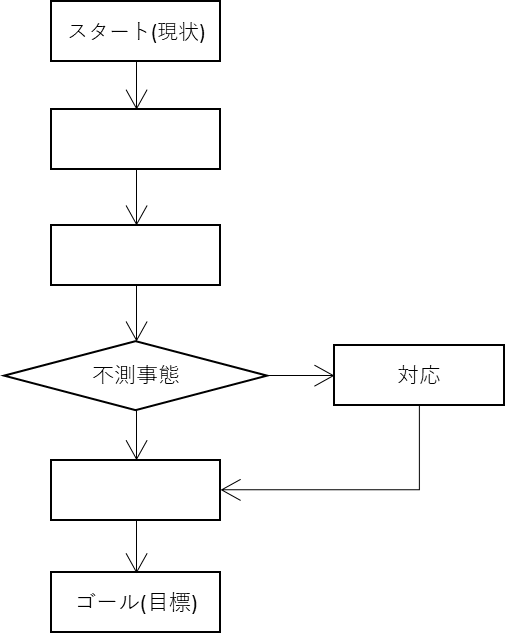 |
| マトリックス図法 | 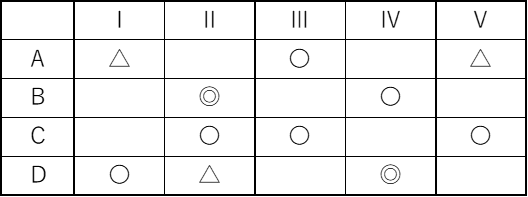 |
| マトリックス データ解析法 | 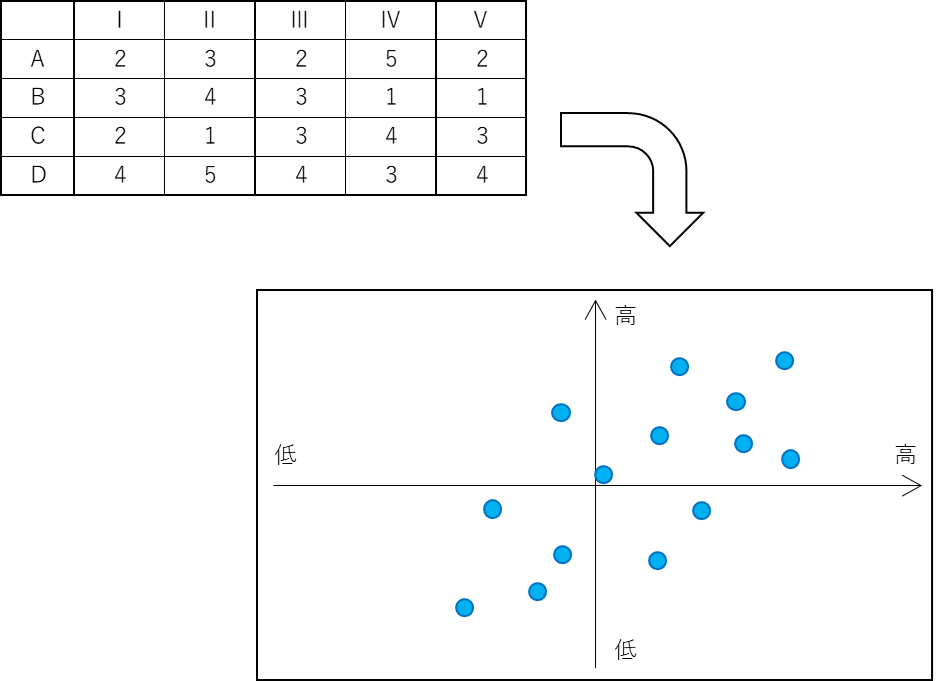 |
こちら詳細に解説していますので、是非ご覧下さい。
統計的方法の基礎【定義と基本的な考え方】
QC検定3級の統計的方法の基礎では、正規分布と二項分布が試験範囲になります。
正規分布と二項分布ともに計算問題が出題されます。
正規分布の計算方法や二項分布については、冒頭の公式をまとめた記事や以下の統計的方法の基礎の記事をご覧下さい。
正規分布 標準偏差
正規分布とは確率分布の一種で、平均値を中心に左右対称な釣鐘型の形状が一般的です。
正規分布のバラツキ表す指標を標準偏差と言います。また標準偏差はσ(シグマ)と表します。
具体的には、データが平均値(μ・ミュー)の周りでどれだけ分散しているかを示します。
こちらはμ(平均値)から±σなら約68.3%、±2σなら約95.4%、±3σなら約99.7%の割合(確率)で合格します。
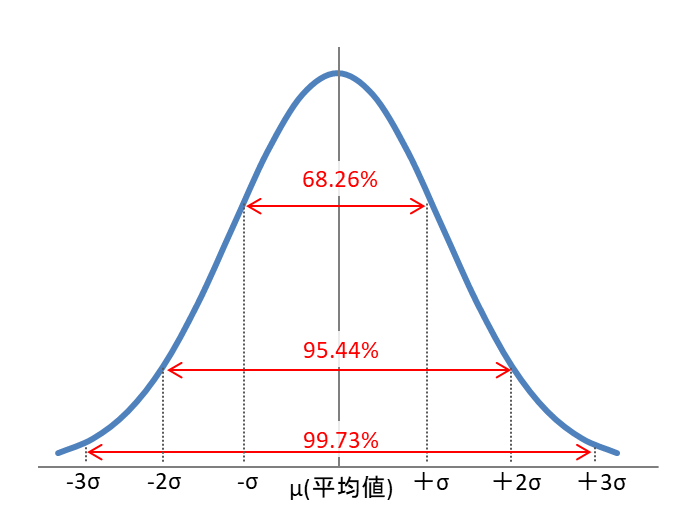
こちらの数値は覚えておきましょう。
| σ | 合格率 | 不適合率 |
|---|---|---|
| ±σ | 約68.3% | 約31.7% |
| ±2σ | 約95.4% | 約4.6% |
| ±3σ | 約99.7% | 約0.3%(1000個中3個) |
| ±4σ | 約99.994% | 約0.00006%(10万個中6個) |
正規分布 表記
正規分布は平均値μと標準偏差σで構成されるので、以下のように表記されます。

例えばN( 20 , 1.52 )と表記されていれば、平均値μは20、標準偏差σは1.5になります。
統計的方法の詳細な解説や練習問題はこちらにありますので、是非ご覧下さい。
管理図
管理図とは品質のバラツキが安定な状態か確認する為の手法です。
またバラツキが安定状態でない場合、その不安定な状態が偶発的なのか、工程の異常なのか判断する事ができます。
QC検定3級での出題傾向は、計算がメインになりますが今回は省略していますので、確認されたい方は冒頭の公式をまとめた記事や以下のQC七つ道具 管理図の記事をご覧下さい。
管理図の種類
管理図は数種類ありますが、QC検定3級ではほとんどXーR管理図のみが出題されます。
時々、文章問題でp管理図とnp管理図が出題される事もありますが、p管理図は不適合率(不良率)、np管理図は不適合数(不良数)の管理状態を確認すると覚えておけば十分だと思います
管理図の見方
管理図で工程に異常が有るか無いかを判断する事ができます。
管理図が正常な状態を「管理状態にある」と言い、管理図に異常の可能性がある状態を「管理状態にない」と言います。
管理状態にないパターンじは色々とありますが、少なくとも以下の2つは覚えておきましょう。
打点がUCL、LCLを超えている
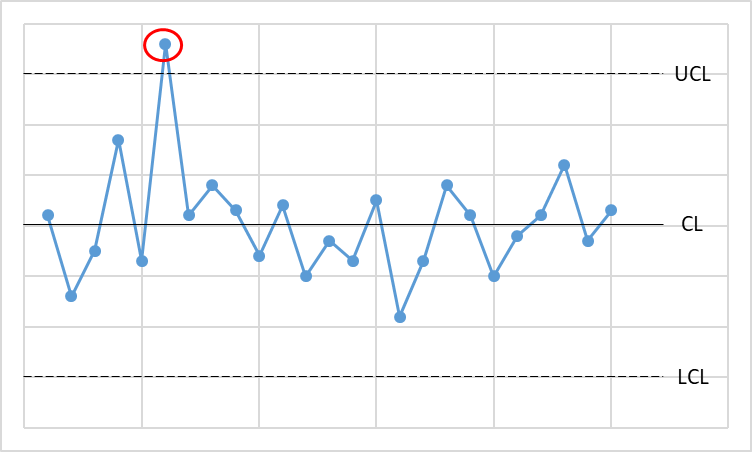
1点でもUCLを越えている場合、またはLCLを下回っている場合は、異常の可能性があります。
長さが9以上の連がある
連とは中心線をまたがず、上側または下側に打点が続いている事を言います。
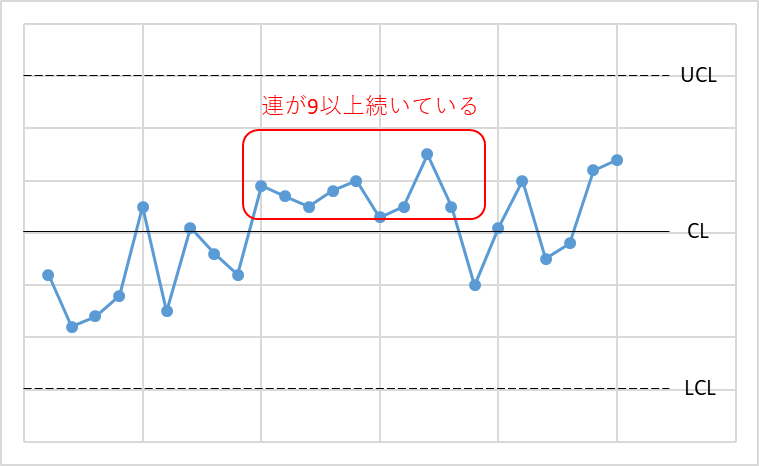
上図のように連が9以上続いている場合も、バラツキにクセがあると判断します。
管理図の詳細な解説や練習問題はこちらにありますので、是非ご覧下さい。
工程能力指数
工程能力指数とは、ある工程が、設計仕様(規格)を満たす製品をどれだけ安定して生産できるかを示す指標です。
工程能力指数では計算問題も出題されますが、冒頭の公式をまとめた記事や以下の工程能力指数(標準偏差)の記事をご覧下さい。
Cp
Cpは工程のバラツキが規格幅に対して、どの程度収まるかを評価します。
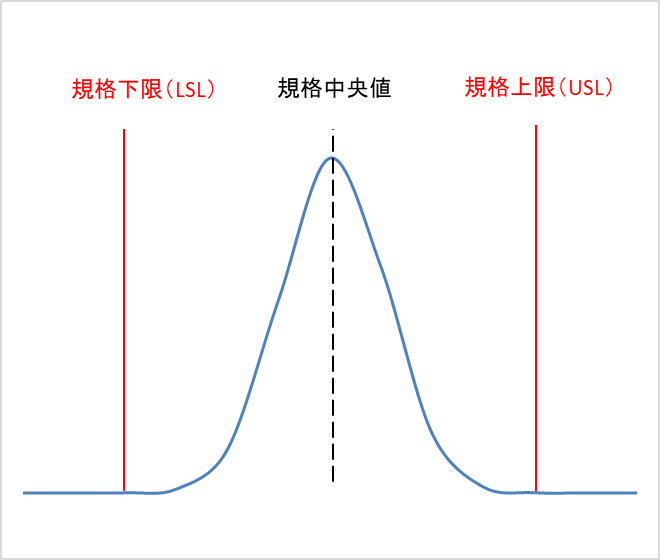
Cpのデータ分布の中心は、必ず規格中央値と同じになります。
仮に測定を行った母集団が規格から外れていたとしても、測定結果のバラツキが小さければCp値は高くなります。
Cpk
工程のバラツキに加え、データ分布の中心が規格中央値からどれだけズレがあるかも評価しています。
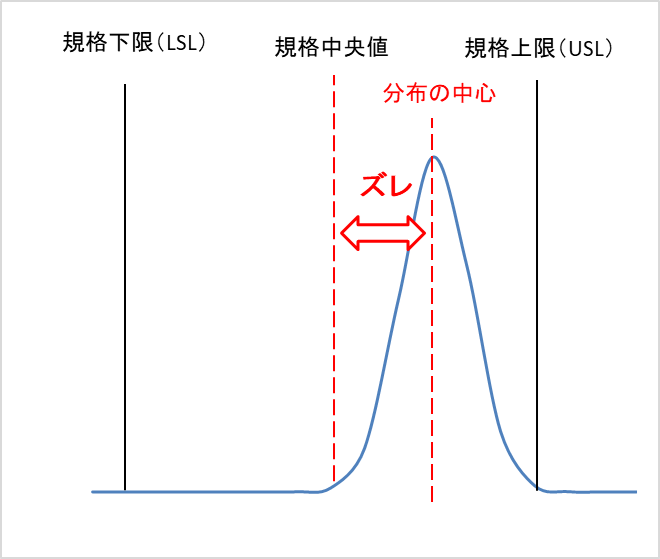
工程のバラツキが小さく、測定結果が全て規格内であっても、データ分布の中心と規格中央値のズレが大きければCpk値は低くなります。
Cp、Cpkの評価
CpとCpkの値で、その工程の生産能力の指標になります。
Cp(Cpk)の値に対して、生産能力や必要な対応は以下の通りです。
| Cp(Cpk) | 工程能力 | 対応 |
|---|---|---|
| Cp≧1.67 | 工程能力は十分過ぎる | バラツキがもう少し大きくなっても心配ないので、管理の省略化やコスト低減方法を検討。 |
| 1.67>Cp≧1.33 | 工程能力は十分 | 理想的な状態なので維持する。 |
| 1.33>Cp≧1.00 | 工程能力は十分とは言えないが、まずますである | 工程管理をしっかりと行い管理状態に保つ。 Cpが1に近づくと不適合品発生の恐れがあるので、必要に応じて対応する。 |
| 1.00>Cp≧0.67 | 工程能力は不足している | 不適合品が発生している。 全数検査や工程管理の改善が必要。 |
| 0.67>Cp | 工程能力は非常に不足している | とても品質を満足する状態ではないので、原因を追及し品質改善を行い、緊急対策が必要。または規格を再検討する。 |
またCp(Cpk)においての不良発生確率は以下の通りです。
| Cp(Cpk) | S(σ) | 不良発生率 |
|---|---|---|
| Cp=0.67 | ± 2σ | 約4.6% |
| Cp=1.00 | ± 3σ | 約0.3% |
| Cp=1.33 | ± 4σ | 約0.006% |
| Cp=1.67 | ± 5σ | 約0.00006% |
工程能力指数の詳細な解説や練習問題はこちらにありますので、是非ご覧下さい。
手法編の要点のまとめはここまでになります。
実践編をまとめた記事もありますので、是非ご覧下さい。












コメント