こちらの記事では、QC検定3級「手法編の公式」をまとめております。
これから手法編を勉強するのにまずは公式を覚えたい方や、試験直前に最後の見直しをしたい方は是非ご活用下さい。
この記事は、公式と覚える出題率を掲載しています。
解き方や練習問題はその都度リンクも張っておりますので、良ければそちらもご覧下さい。
データの取り方・まとめ方の計算式
データの取り方・まとめ方の公式は下表の通りです。
| 項目 | 公式 | 出題頻度 |
|---|---|---|
| 平均値 X | 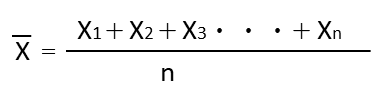 | ☆☆☆☆☆ |
| 平方和 S | 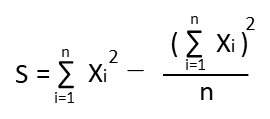 | ☆☆ |
| 分散 V | 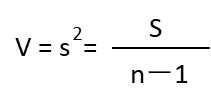 | ☆☆☆ |
| 標準偏差 s | 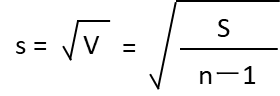 | ☆☆☆☆ |
| 範囲 R | R = Xmax- Xmin | ☆☆☆☆ |
| 変動係数 CV | 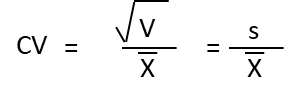 | ☆ |
QC検定3級では平均値、標準偏差、範囲が出題され易いです。
平均値は問題無いと思いますので、まずは簡単に解ける範囲(Xmax- Xmin)を理解し、次に標準偏差を解けるようにしておきましょう。
しかしながら、それ以外の平方和と分散も出題頻度が少ない訳ではありません。
また、平方和なら相関分析のSxxやSyyで使用され、分散なら標準偏差とセットで出題される可能性があるので、やはり覚えておきましょう。
変動係数についてはほとんど出題されないので、余裕があれば覚えるくらいでいいと思います。
上記の公式にはありませんが、メディアン(Me)も一緒に出題されるので、こちらも理解しておきましょう。
具体的な解き方や練習問題のありますので、こちらも是非ご覧下さい。
統計的方法の基礎【定義と基本的な考え方】の計算式
統計的方法の基礎の公式は下表の通りです。
| 項目 | 公式 | 出題頻度 |
|---|---|---|
| Kp(正規分布) |  | ☆☆☆☆ |
| 確率p(二項分布) | 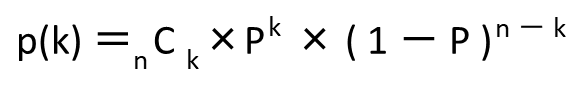 | ☆☆ |
QC検定3級ではKp(正規分布)が出題され易いです。
確率p(二項分布)は出題頻度が少ないので、まずはKp(正規分布)を解けるようにしておきましょう。
具体的な解き方や練習問題はこちらになります。是非ご覧下さい。
管理図の計算式
管理図の公式は下表の通りです。
| 項目 | 公式 | 出題頻度 |
|---|---|---|
| X管理図 | ||
| 上部管理限界UCL | 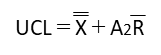 | ☆☆☆☆☆ |
| 中心線CL | 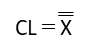 | ☆☆ |
| 下部管理限界UCL | 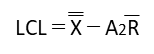 | ☆☆☆☆☆ |
| R管理図 | ||
| 上部管理限界UCL | 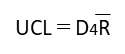 | ☆☆☆☆☆ |
| 中心線CL | 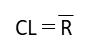 | ☆☆ |
| 下部管理限界UCL | 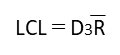 | ☆☆ |
管理図ではX管理図のUCL・LCLとR管理図のUCLの出題され易いです。
ただし、X管理図・R管理図ともにUCL・LCLの計算にはCLの値を使用するので、基本的には全て覚えておきましょう。
※管理図の問題は毎回出題され、計算問題の出題頻度も多いです。
具体的な解き方や練習問題はこちらになります。是非ご覧下さい。
相関分析の計算式
相関分析の公式は下表の通りです。
| 項目 | 公式 | 出題頻度 |
|---|---|---|
| 相関関数r | 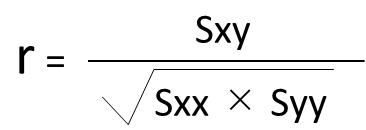 | ☆☆☆☆ |
| Sxy | 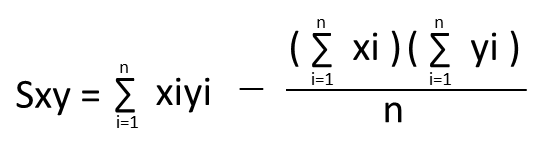 | ☆☆ |
| Sxx | 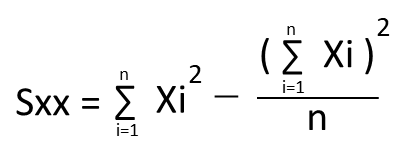 | ☆ |
| Syy | 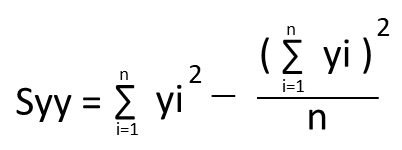 | ☆ |
相関分析では相関係数rが出題され易いです。
Sxy、Sxx、Syyの数値は問題文で書かれている事が多いので、まずは相関係数rの公式を覚える事をおすすめします。
ただし、SxxとSyyは「データの取り方・まとめ方」の平方和Sと同じで、Sxyも考え方は同じなので、やはり覚えておく事をおすすめします。
具体的な解き方や練習問題はこちらになります。是非ご覧下さい。
工程能力指数の計算式
工程能力指数の公式は下表の通りです。
| 項目 | 公式 | 出題頻度 |
|---|---|---|
| Cp | 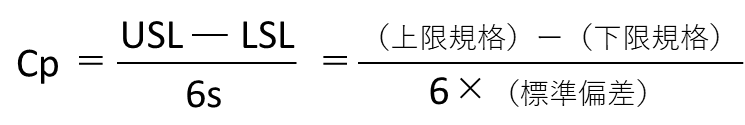 | ☆☆ |
| Cpk (平均値>規格中央値) | 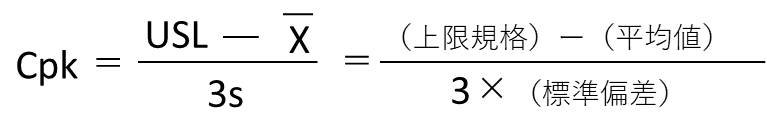 | ☆☆ |
| Cpk (平均値<規格中央値) |  | ☆☆ |
QC検定3級では工程能力指数の出題頻度が2回1度ぐらいなので、Cp・Cpk計算問題の出題頻度も少なくなります。
この問題を捨てるのはもったいないですが、まずは「データの取り方・まとめ方」や「管理図」などを優先して、余裕ができてから工程能力指数を理解する事をおすすめします。







コメント