この記事では、QC検定3級のテスト対策として新QC七つ道具の練習問題を記載しています。
良ければ、練習として解いてみて下さい。
QC検定3級向けの新QC七つ道具の解説は以下の記事で投稿しておりますので、よければご覧ください。
練習問題
問1 文章問題
以下の(a)~(e)はそれぞれ新QC七つ道具の手法について説明を行っている。それぞれ何手法について説明しているか、下の選択肢から選びなさい。
(a)
言語データを類似性によってグルーピングし、図にまとめる事で問題の構造や本質を理解する手法。
(b)
現状から目標の事項をフローチャートにし、不測事態と対応を先に考えてリスク回避する手法。
(c)
複雑に絡み合っている問題を結果と原因(目的と手段)の関係を、論理的に展開する事により、シンプルにして問題を解明する手法。
(d)
2つの事象の項目を行と列の二元表にし、それぞれの交点の関係を記号化する事によって、必要な情報を得る手法。
(e)
計画(プロジェクト)を推進する上で必要な作業手順を整理したり、進捗管理するのに有効な手法。
(f)
達成すべき目標に対する方策を1次手段、2次、3次と多段階に展開する事で、具体的に目標達成に有効な方策を求める手法。
(g)
マトリックス図でまとめた数値データをを主成分分析によって縮約する手法。
【選択肢】
ア:PDPC法 イ:マトリックス・データ解析法
ウ:管理図法 エ:連関図法
オ:系統図法 カ:親和図法
キ:アローダイヤグラム法 ク:マトリックス図法
コ:特性要因図法
問2 穴埋め問題
系統図法
a~fに合う語句を選択肢ア~キより選びなさい。
【a】の設定を起点として、その【a】を達成するために必要な手段を体系的に整理・構造化する図です。問題や【b】の原因を見極めながら、それぞれの要素を一次、二次、三次へと段階的に【c】することで、思考の抜け漏れを防ぎ論理的なアプローチを可能にする事で、具体的に目標達成に有効な【d】を求める事ができる手法です。
また、系統図に以下の2種類あります。
【e】:【a】と手段の関係を枝分かれさせながら展開する。
【f】:対象を構成する要素に展開する。
【選択肢】
ア:方策 イ:課題
ウ:展開 エ:目的
オ:構成要素展開型 カ:方策展開型
連関図法
g~hに合う語句を選択肢キ~コより選びなさい。
連関図法は、【g】に対して、その結果と原因の【h】を論理的に展開し、問題と原因の構造を探る手法です。
【選択肢】
キ:独立性 ク:関係性
ケ:シンプルな構造 コ:複雑に絡み合った問題
親和図法
i~kに合う語句を選択肢サ~タより選びなさい。
親和図法とは、事実・意見・発想などの【i】を収集し、それらの持つ【j】に着目して整理し、関連性の高いものを【k】することで、問題の本質や解決策の方向性を見出す手法です。
【選択肢】
サ:数値データ シ:引き離し
ス:言語データ セ:グルーピング
ソ:独創性 タ:類似性
問3 図形
以下の新QC七つ道具の図(a)~(g)に合う名称ア~キより選びなさい。
(a)
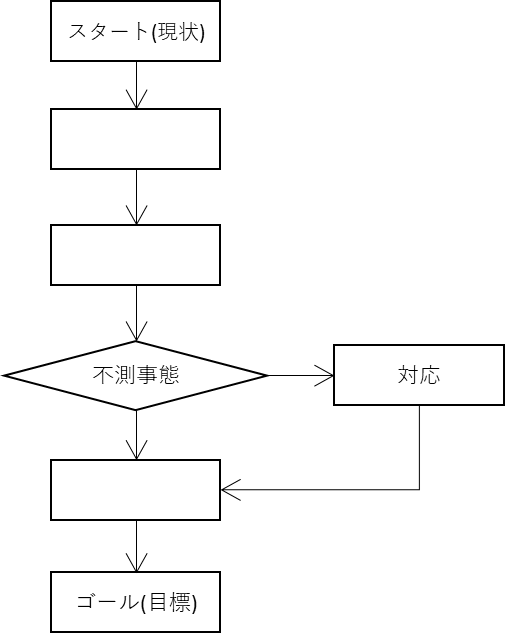
(b)
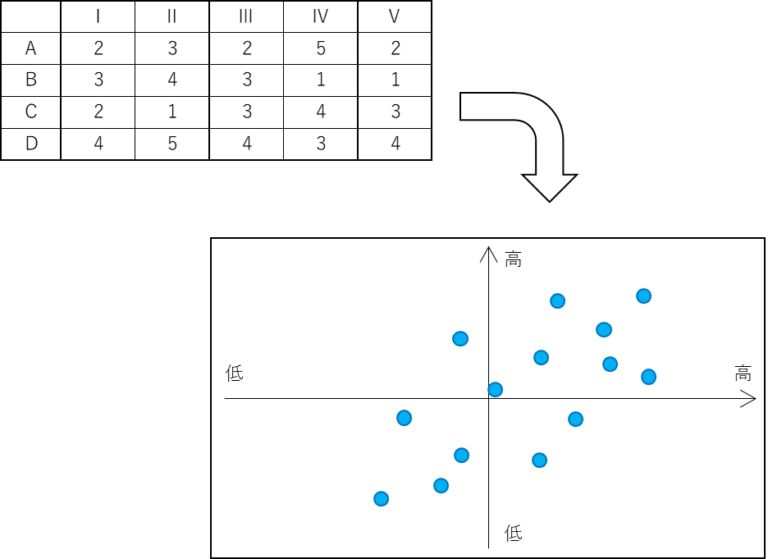
(c)
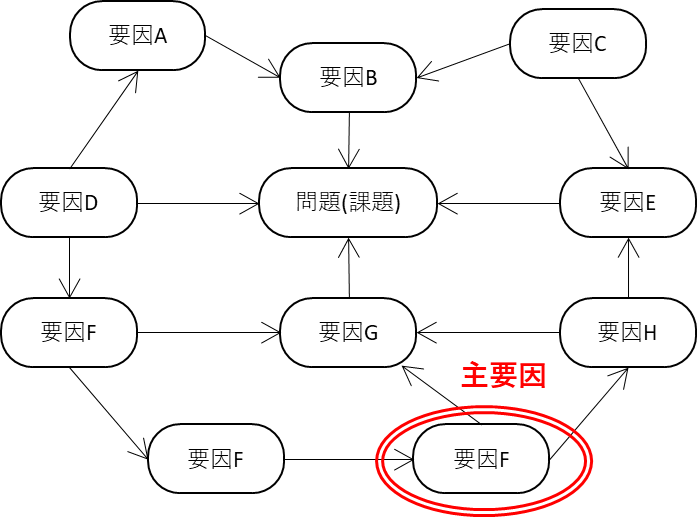
(d)
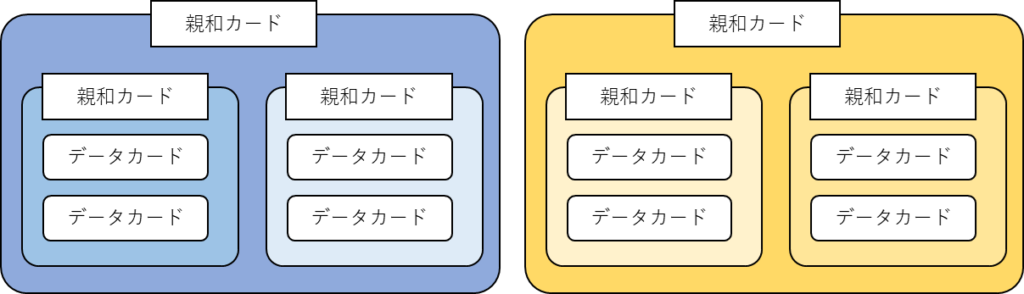
(e)
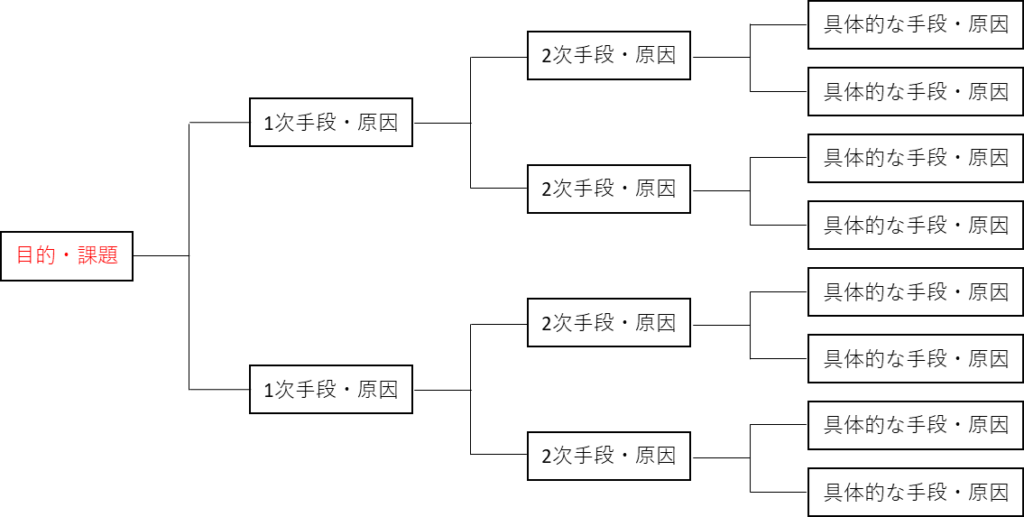
(f)
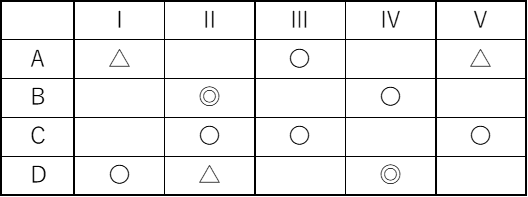
(g)
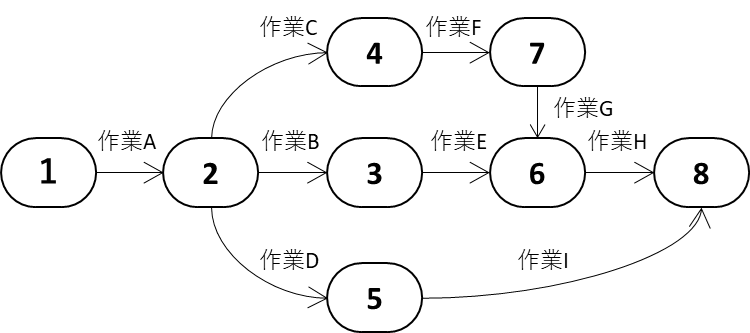
【選択肢】
ア:系統図法 イ:連関図法
ウ:親和図法 エ:アローダイアグラム法
オ:PDPC法 カ:マトリックス図法
キ:マトリックスデータ解析法
解答
問1 文章問題
説明文に対して、新QC七つ道具の図法を結びつける問題では、各図法の特徴になるワードを覚えておくと回答を選び易くなります。
【解答】
(a) カ:親和図法 (b) ア:PDPC法
(c) エ:連関図法 (d) ク:マトリックス図法
(e) キ:アローダイヤグラム法
(f ) オ:系統図法
(g) イ:マトリックス・データ解析法
(a)親和図法
親和図法とは、ある問題や課題に関する様々な情報(言語データ)を収集し、それらを「親和性(似ている、関係が強いなど)」によってグループに分け、図として整理していく手法です。
今回のような文章問題や穴埋め問題は、(事実、意見、発想などの)言語データ、親和性、類似性、グルーピング(グループ化)と言ったワードが出題し易いです。
(b)PDPC法
PDPC法とは、目標達成までの過程で起こりうる不測の事態やトラブルを事前に予測し、それに対する対策や代替案を検討・明確にするための手法です。
文章問題や穴埋め問題では、フローチャートにする(フロー化)、不測の事態を予想する(リスク回避)、目標に至るプロセス(ルート)を決めると言ったワードが出題し易いです。
(c)連関図法
連関図法は、複雑に絡み合った問題に対して、その結果と原因の関係性を論理的に展開し、問題と原因の構造を探り問題を解明する手法です。
文章問題や穴埋め問題では、複雑に絡み合った問題、目的と手段(結果と原因)、論理的に展開と言ったワードが出題し易いです。
(d)マトリックス図法
マトリックス図法とは2つの事象の項目を行と列の二元表にし、それぞれの交点の関係を記号化する事によって、必要な情報を得る手法です。
文章問題や穴埋め問題では、2つの事象、縦列と横列(行と列)、二元表、記号化、それぞれの交点と言ったワードが出題し易いです。
(e)アローダイヤグラム法
アローダイヤグラム法とは、計画(プロジェクト)を推進する上で必要な作業手順を整理したり、進捗管理するのに有効な手法です。
文章問題や穴埋め問題では、プロジェクト、(最適な)日程管理、進捗管理、ネックとなる作業の抽出と言ったワードが出題し易いです。
(f)系統図法
系統図法とは、目標達成のための手順や解決策を、段階的に細分化してツリー状に展開して求める手法です。
文章問題や穴埋め問題では、方策、目標達成、1次・2次・3次手段、展開と言ったワードが出題し易いです。
また系統図法は主に以下の2種類に分類されます。時々出題されるので、覚えておきましょう。
方策展開型 : 目的と手段の関係を多段階的に枝分かれさせながら展開する。
構成要素展開型 : 対象を構成する要素に展開(分解)し整理する。
(g)マトリックス・データ解析法
マトリックス・データ解析法とは、複数の評価項目を整理・縮約し、視覚的に傾向や関係性を把握するための手法です。
文章問題や穴埋め問題では、数値データ(新QC七つ道具では唯一)、マトリックス図法と言ったワードが出題し易いです。
問2 穴埋め問題
こちらの問題では、新QC七つ道具について特徴などを理解しているかが問われています。
特にQC検定3級では系統図法、連関図法、親和図法が出題し易いです。
系統図法
【解答】
[a] エ:目的 [b] イ:課題
[c] ウ:展開 [d] ア:方策
[e] カ:方策展開型
[f ] オ:構成要素展開型
問題文に解答を当てはめると以下の通りになります。
【a:目的】の設定を起点として、その【a:目的】を達成するために必要な手段を体系的に整理・構造化する図です。問題や【b:課題】の原因を見極めながら、それぞれの要素を一次、二次、三次へと段階的に【c:展開】することで、思考の抜け漏れを防ぎ論理的なアプローチを可能にする事で、具体的に目標達成に有効な【d:方策】を求める事ができる手法です。
また、系統図に以下の2種類あります。
【e:方策展開型】:目的と手段の関係を枝分かれさせながら展開する。
【f:構成要素展開型】:対象を構成する要素に展開する。
連関図法
【解答】
[g] コ:複雑に絡み合った問題 [h] ク:関係性
問題文に解答を当てはめると以下の通りになります。
連関図法は、【g:複雑に絡み合った問題】に対して、その結果と原因の【h:関係性】を論理的に展開し、問題と原因の構造を探る手法です。
親和図法
【解答】
[i ] ス:言語データ [j ] タ:類似性
[k] セ:グルーピング
問題文に解答を当てはめると以下の通りになります。
親和図法とは、事実・意見・発想などの【i:言語データ】を収集し、それらの持つ【j:類似性】に着目して整理し、関連性の高いものを【k:グルーピング】することで、問題の本質や解決策の方向性を見出す手法です。
問3 図形
QC検定3級では新QC七つ道具の図形と名称を問われる問題も時々出題されます。図形のイメージはその手法の特徴も覚えやすくなるので、こちらの問題は確実に解けるようにしておきましょう。
【解答】
(a) オ:PDPC法 (b) キ:マトリックスデータ解析法
(c) イ:連関図法 (d) ウ:親和図法
(e) ア:系統図法 (f ) カ:マトリックス図法
(g) エ:アローダイアグラム法
(a) PDPC法

(b) マトリックスデータ解析法

(c) 連関図法

(d) 親和図法

(e) 系統図法

(f) マトリックス図法

(g) アローダイアグラム法

練習問題に慣れたら、次は過去問にチャレンジしましょう。



コメント