QC七つ道具 ヒストグラム

ヒストグラムとはQC七つ道具の1つで、品質特性値のバラツキをデータの分布で表し、規格値との関係や不適合発生状況などを視覚的に認識するための手法です。

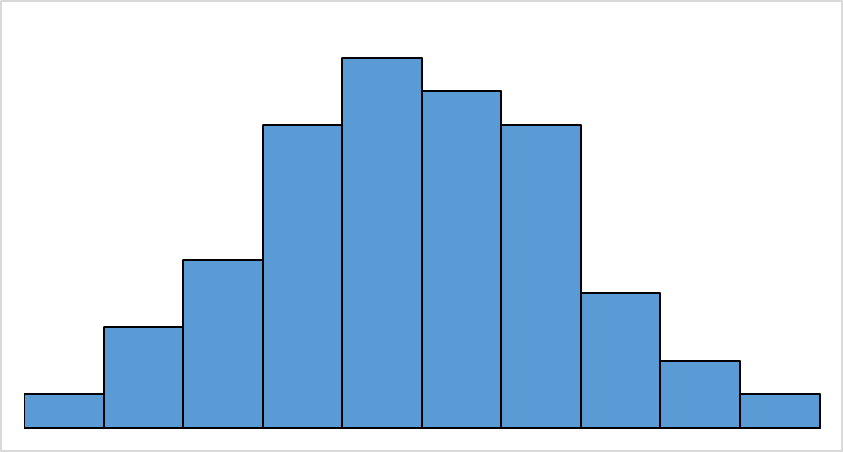
縦軸に度数、横軸に区間分けしたデータで作成した棒グラフになります。
※度数・・・区間の幅に当てはまる測定値の数

第24回～第30回のQC検定3級では以下のように出題されます。

試験(QC検定3級)	第24回	第25回	第26回	第27回	第28回	第30回
ヒストグラム	1問	×	×	2問	1問	1問

管理図は第24回～第30回のQC検定3級では約70%の確率で出題されます。

出題傾向としては、データの分布の形から品質状態について考察したり、規格上下限との関係がよく出題されます。

ヒストグラフの使い方・見方

ヒストグラムでの考察方法を説明します。

①分布の形をつかむ

ヒストグラムの分布は品質状態や工程の状態で様々な形になるので、分布の形を把握する事が重要になります。

分布の形は以下の通りです。

一般型

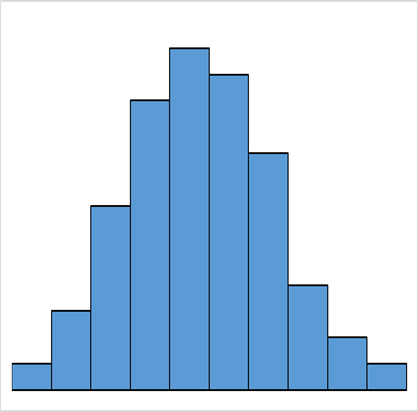
中心近く中心近くが一番高く、両端へ離れていくにつれて徐々に低くなります。
また、左右対称に近い形になります。

工程が安定している時に、この形になります。

歯抜け型

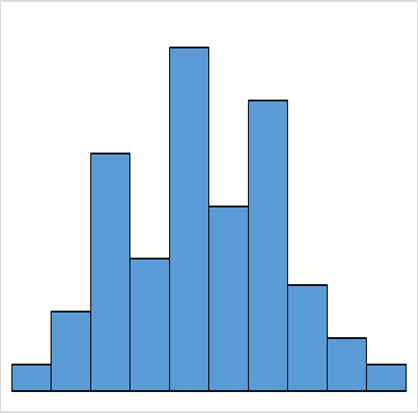
一般型に比べ、部分的に度数が低くなっています。

区間幅の設定値に問題があったり、測定者の測定方法や読み方にクセがある場合などに現れます。

すそ引き型

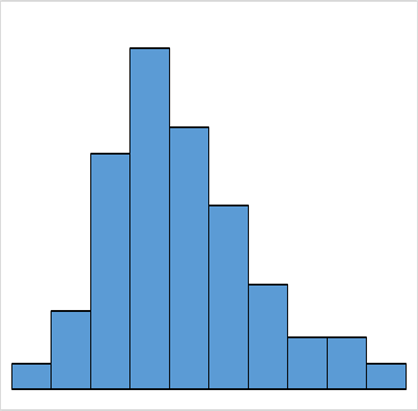
平均値が中心より左や右寄りになっています。
また、左右非対称になります。
上下限が抑えられている場合に現れます。特に左寄り場合は中心が0付近で、マイナスが無い場合に現れます。

絶壁型

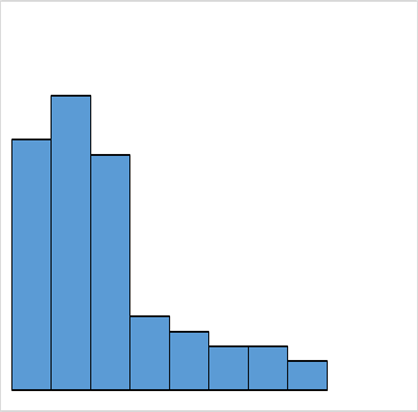
平均値が極端ひ左や右に寄りになっています。
度数が急に低くなだらかになっているのも特徴です。

規格外を選別で取り除いた場合や、測定のごまかしや測定ミスなどにも現れます。

高原型

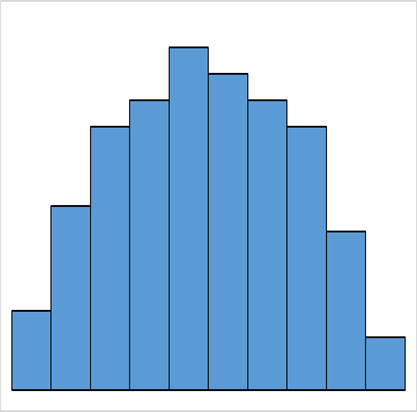
一般型と比べ、各区間の度数の起伏がなだらかになっています。

平均値が異なる複数の分布が混ざっている場合に現れます。
層別を行い、分布を分ける必要があります。

ふた山型

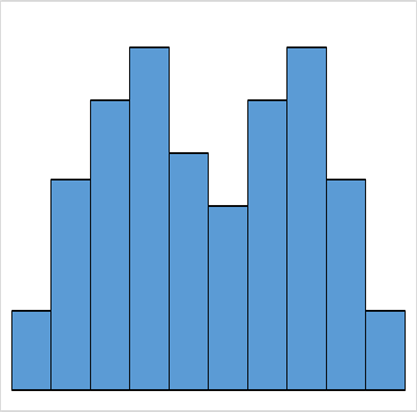
中心近くの度数が低くなり、山が2つあります。

平均値が異なる2つの分布が混ざっている場合に現れます。
高原型と同様に層別を行い、分布を分ける必要があります。

離れ小島型

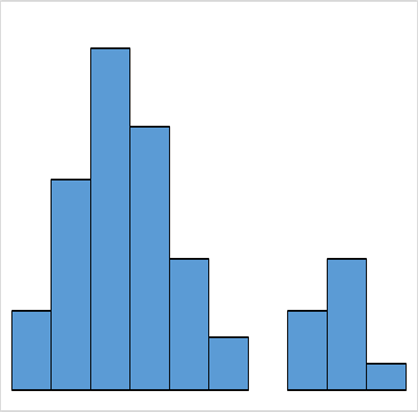
右端、または左端に小さな分布があります。

異なった分布のデータが少量混ざっていると現れます。
また、ロット内で部分的に異常が発生していた場合にも現れます。

②バラツキやかたよりの原因を調べる

一般型以外の分布や中心にかたよりが見られる場合は、工程に異常がある可能性があるので、その原因を調べる必要があります。

※測定の不備やサンプルの取り方に問題がある場合もあります。

③規格と比較して問題がないか調べる

規格と比較する事で、技術的要求を満たしている事や生産の実力を確認する事ができます。

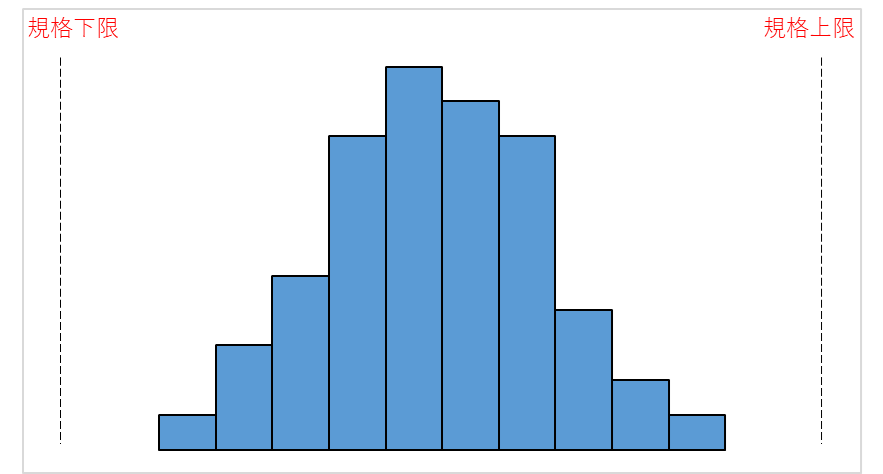
上図は規格に対して、理想的なバラツキ方と言えます。

規格内でも、理想的でないバラツキ方があります。

バラツキ方	分布の特徴	処置
片側に寄っている	バラツキの幅は理想に近いが、上下限どちらかに寄っている	分布の平均値を中心に近づくように工程を調整する
規格上下限に余裕がない	理想な分布に対してバラツキの幅が広く、規格内だが上下限近くまで分布が広がっている	バラツキの幅が広くなる原因を調査し対策する
規格上下限に余裕があり過ぎる	理想な分布に対してバラツキの幅が狭く、分布と規格上下限までの隙間が大きい	規格上下限の幅を狭くする。または、工程の一部を省力化するなど、コストダウンを図る。 ※加工数を減らす、検査を省く、生産速度を上げるなど。

規格を満たしていない場合も、もちろん異常なので工程の調査をしなければいけません。
この場合もどうやって規格から外れているのか、バラツキ方を確認してから調査を行います。

④対策前後で効果確認する

対策前後のヒストグラムを比較し、効果を確認します。
バラツキ方や分布の平均値の位置が対策後、理想に近づいている事を確認する。

ヒストグラムの作り方

QC検定3級で出題される可能性は低いですが、ヒストグラムを理解するには、ヒストグラムの作成方法を理解する事をおすすめします。

大根の長さを例にして、ヒストグラムの作成方法を説明します。

①目的を明確にする

大根を運搬する為に、箱を準備しないといけません。
箱の大きさを決めたいので、大根の長さのバラツキを調査します。

②データを収集する

大根の長さを測定し、記録を取っていきます。
ヒストグラムを作成する時は、データ数(n)を100以上取る事が望ましいです。

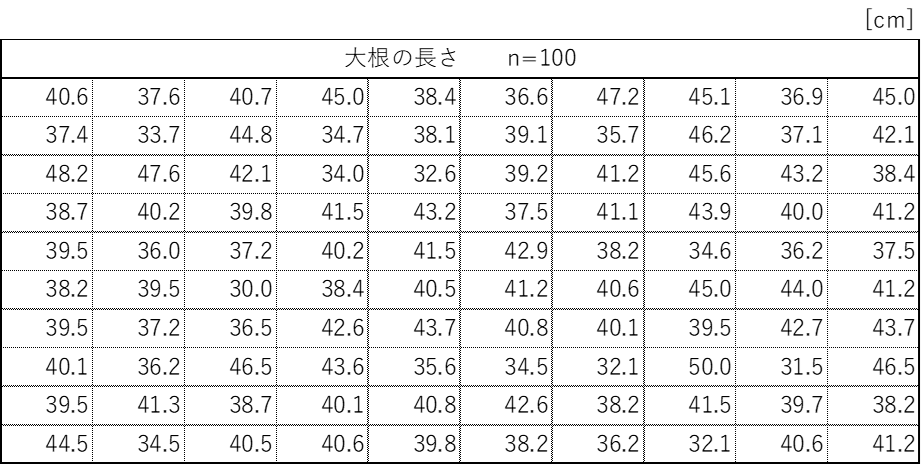
今回のデータ数はn=100です。

③データの最大・最小を求める

測定値の中から、最大値と最小値を求めます。

最大値(L)＝50cm
最小値(S)＝30cm

④仮で区間数を決める

区間数を決める方法は色々とありますが、以下の公式で計算して決める事が多いです。

　k(区間数)＝√n(データ数)

今回はデータ数が100個なので、k＝√100＝10になります。
計算結果が整数でない場合は、小数点は切り捨てします。

この区間数は仮で決めたものです。
度数分布表作成などの時に区間数が増減する事があります。

⑤区間幅を決める

区間幅は以下の公式で求めます。

　区間幅(ｈ)＝［最大値(L)－最小値(S)］／区間数(k)

今回の区間幅は
ｈ＝（50－30）／ 10 ＝ 2　になります。

⑥区間の境界値を決める

区間の境界値とは、棒グラフの重なる位置の事です。
各区間の境界値を求めるのに、まずは第1区間の下限境界値と上限境界値を以下の公式で、求める必要があります。

　第1区間の下限境界値＝最小値ー区間幅/2

　第1区間の上限境界値＝最小値＋区間幅/2

今回の境界値は以下の通りになります。
第1区間の下限境界値＝ 30 ー 2/2 ＝ 29
第1区間の上限境界値＝ 30 ＋ 2/2 ＝ 31

区間の中心値も計算します。
中心値は上限境界値と下限境界位置の真ん中になります。

今回の第1区間の中心値は
31－29＝30になります。

⑦度数分布表の作成

先程求めた第1区間の下限・上限境界値、中心値から度数分布表を作成します。
第2区間以降は区間幅分を追加していきます。

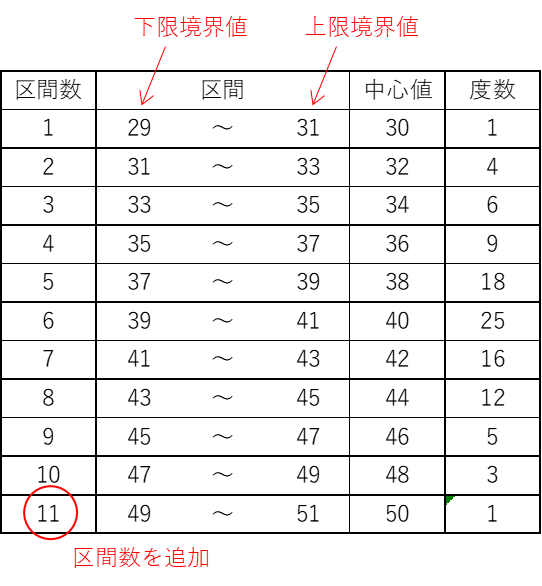
また仮で決めた区間数は10ですが、その場合、最大値49までとなり、最大値50は収まらないので、区間数を11で決定しました。

⑧ヒストグラフ作成

作成した度数分布表から、縦軸を度数、横軸を中心値としたヒストグラムを作成します。
各区間の隙間はゼロにします。

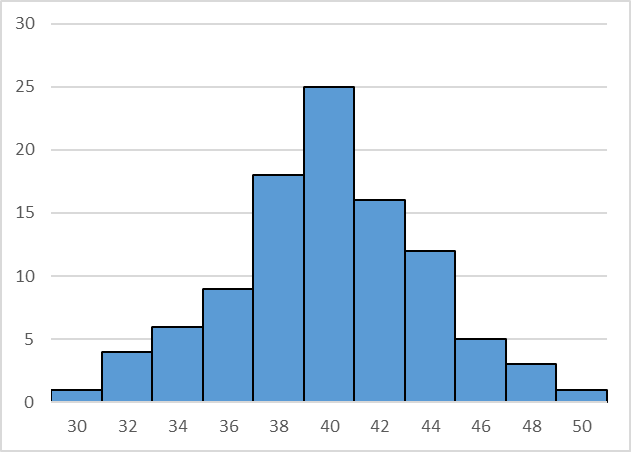
作成したヒストグラムから、分布の形や中心の位置を確認して、工程に異常が無いか考察します。

前の記事
QC検定3級　QC七つ道具　管理図 | アンキロぱぱのブログ (ankiropapa.com)

次の記事
QC検定3級　QC七つ道具　ヒストグラム②　標準偏差と工程能力指数 | アンキロぱぱのブログ (ankiropapa.com)