QC七つ道具の1つである散布図とは、2つの変数の相関関係を視覚化する事を目的とした手法です。
QC検定3級では「散布図から相関係数の大きさを推測する事」や「表から相関の強さや向きを計算する事」などが出題されます。
また第24回～第30回のQC検定3級では以下のように出題されます。
| 試験(QC検定3級) | 第24回 | 第25回 | 第26回 | 第27回 | 第28回 | 第30回 |
| 散布図 | １問 | 1問 | 1問 | １問 | 1問 | 1問 |
QC検定3級では散布図は必ず出題されます。
2回に1回のペースで計算問題も出題されるので、苦手意識がある方もいると思いますが、出題傾向は限られているので、点数に結び付きやすいので是非この記事をご覧下さい。
相関の強さと向き
冒頭でも説明させて頂いた通り、2つの変数の相関関係を調査する為に視覚化を目的とした手法です。
具体的には以下の2つの相関について確認します。
①相関の強さ
分布の形状で、相関の強さも調査できます。
散布図の分布が長細く集中し、1本の線に近くなれば、2つの変数は強い相関があります。
逆に散布図の分布が太く楕円のように散らばると、2つの変数は弱い相関となります。
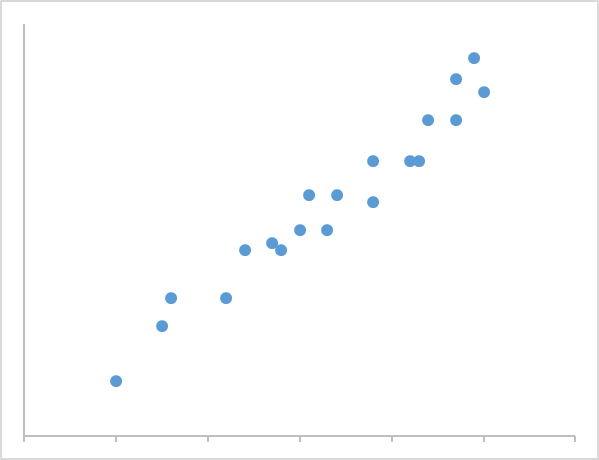
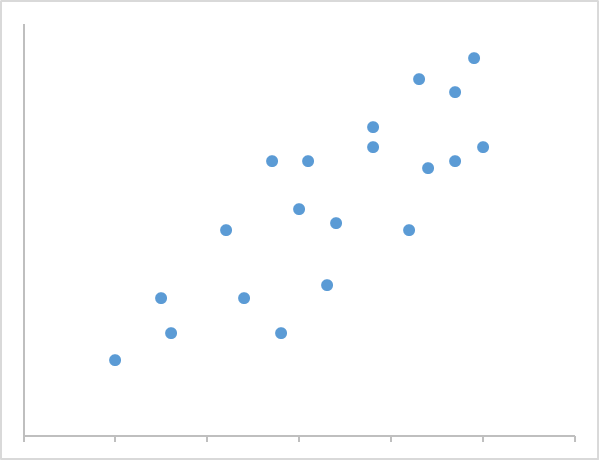
弱い相関より分布が散らばり、相関が見られない事を相関なしと言います。
また、散らばっている分布以外にも、Vの字や放物線のような分布も相関なしとなります。
※逆向きも同様に相関なしになります。
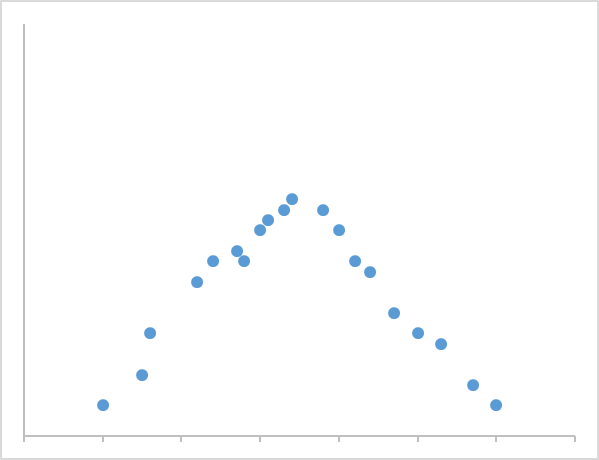
②相関の向き
散布図が右肩上がりの分布は正の相関といいます。
逆に右肩下がりの分布は負の相関といいます。
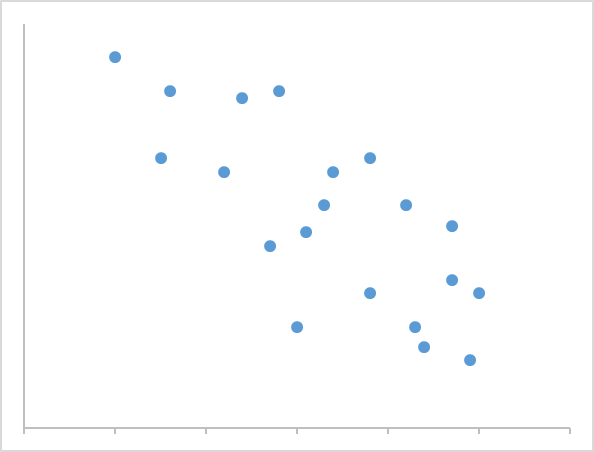
相関の数値化
相関の強さや向きは数値で表す事ができます。これを相関係数[r]と言います。
相関係数[r]は -1 ≦ 0 ≦ 1 の範囲となります。
1に近ければ正の相関は強く、-１に近ければ負の相関が強くなります。また0の場合は相関なしとなります。
また相関係数の数式は以下の通りになります。
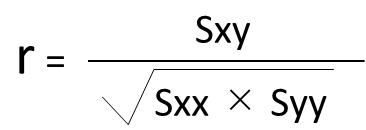
また上記の平方和Sxy、Sxx、Syyの公式は以下の通りになります。
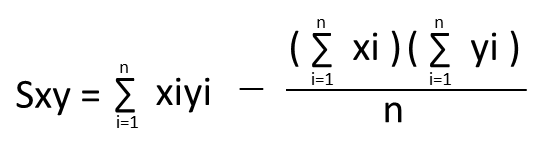
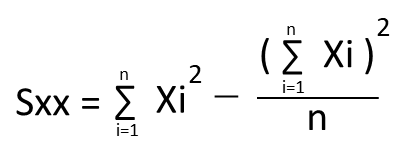
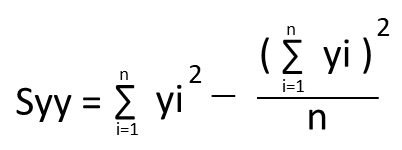
QC検定3級出題傾向
冒頭で説明させて頂いた通り、QC検定3級では「散布図から相関係数の大きさを推測する事」や「表から相関の強さや向きを計算する事」などが出題されます。
①散布図から相関係数の大きさを推測
QC検定では高い確率で「散布図から相関係数の大きさを推測する事」が問われます。
ここを理解しているとその設問の60～100%を正解する事ができ、また計算問題が出題しても選択肢を絞り込んだり、問題によっては正解を予測できる事もあります。
だから時間が無い方も、ここはしっかりと抑えましょう。
以下の例題で具体的に説明します。
例題
以下の散布図（a）～（d）と合う相関係数［r］を選択せよ。
［選択肢］
（ア）0.98
（イ）0.80
（ウ）0
（エ）-0.75
例題 解き方
まず回答は以下の通りになります。
［答え］
（a）エ
（b）ウ
（c）イ
（d）ア
この問題のに2つのポイントがあります。
［ポイント］
・散布図が正の相関、負の相関、相関なしか考える。
・他の散布図と比較し、相関の強さを考える。
具体的には以下の問題を解きます。
まず散布図（a）は右下がりなのでは負の相関であることが分かります。
選択肢で負の相関（r<0）は（エ）のみなので、答えは（エ）になります。
散布図（b）は一見では正の相関か負の相関か分かりません。
だから相関係数が0に近い、あるいは0のどちらかになります。
選択肢では0に近い数値はありませんので、答えは（ウ）になります。
散布図（c）（d）はどちら正の相関なので、それぞれ（ア）と（イ）に絞れます。
散布図（d）は散布図（c）と比べると散らばりが小さく直線に近いので、こちらの方が強い相関なのが分かります。
相関係数の絶対値が大きい方が強い相関なので、散布図（c）は（イ）、散布図（d）は（ア）になります。
②表から相関の強さや向きを計算
QC検定3級の散布図では、2年に１回ぐらいのペースで出題されます。
出題内容はx、yや各2乗、xとyを掛け合わせた一覧表と公式から、最終的に相関係数[r]を計算します。
以下の記事で相関係数の練習問題を投稿しています。
良ければこちらの練習問題を問いてみて下さい。
【補足】
QC検定3級ではあまり出題されませんが、散布図を作成・観察する時は以下の2つについて注意が必要なので参考として記載させて貰います。
①特性と要因
2つの変数が特性（結果）と要因（原因）の場合は、ｙ軸を特性、ｘ軸を要因にします。
【例】
ロット（生産日）毎に対しての不良率で散布図を作成する場合、ｘ軸をロット、ｙ軸を不良率にする
②層別
散布図も層別する事で、情報量が増えたり、見解が変わる事があります。
例えば、層別する事で相関を見つけたり、逆に相関があると思っていたものが層別をする事で相関が無い事に気付く事があります（偽相関）。
偽相関とは、一見相関があるように見えても、実は相関がなく判断ミスさせる散布図の事をいいます。 偽相関を判断するには、散布図の結果を過信せず、２つのデータ（特性と要因など）の関係をしっかりと調査し、考察する事が重要です。
層別についてはこのページで説明しています。
QC検定3級 QC七つ道具 層別 | アンキロぱぱのブログ (ankiropapa.com)
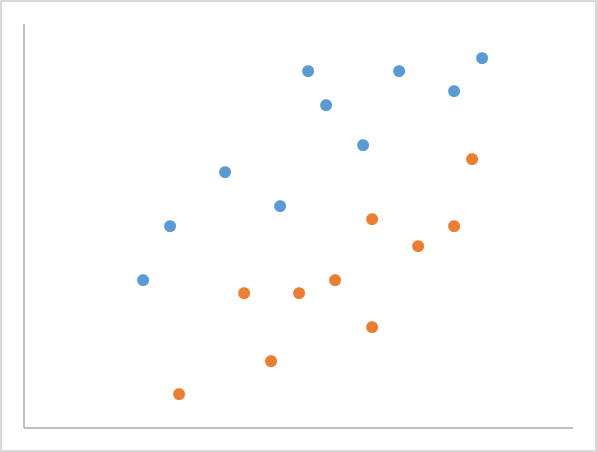
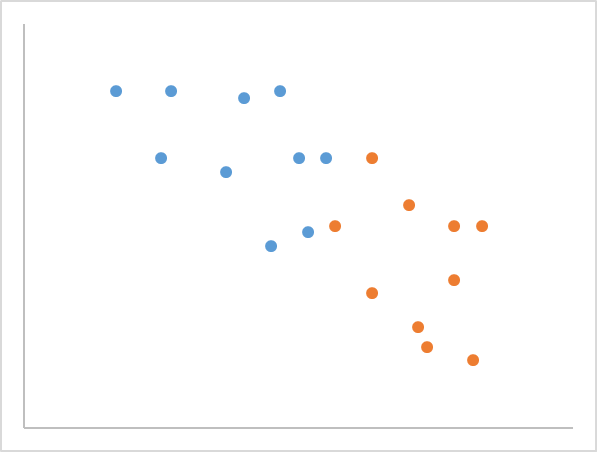
また層別する場合は、同じ散布図内でそれぞれをプロットします。
プロットは色や形（〇、△、✖など）で分けます。
コメント